Question

How do you evaluate sine, cosine, tangent of `-pi/6` without using a calculator?

Answer 1

`sin(-pi/6)=-1/2`
`cos(-pi/6)=sqrt2/2`
`tan(-pi/6)=-sqrt3/3`

Explanation:

Recall that:
`sin(-x)=-sin(x)`
`cos(-x)=cos(x)`
`tan(-x)=-tan(x)`

and,
`pi/6`/`(30^@)` is a special angle.

Hence,
`sin(-pi/6)=-sin(pi/6)`
`color(white)(xxxxx....)=-1/2`

`cos(-pi/6)=cos(pi/6)`
`color(white)(xxxxxx..)=sqrt2/2`

`tan(-pi/6)=-tan(pi/6)`
`color(white)(xxxxxx..)=-sqrt3/3`

Answer 2

`sin(-pi/6)=-1/2`
`cos(-pi/6)=sqrt(3)/2`
`tan(-pi/6)=-1/sqrt(3)=-sqrt(3)/3`

Explanation:

Draw an equilateral triangle with unit lengths. Each angle is `pi/3`.

Now, bisect one of the angles. This gives two right triangles.

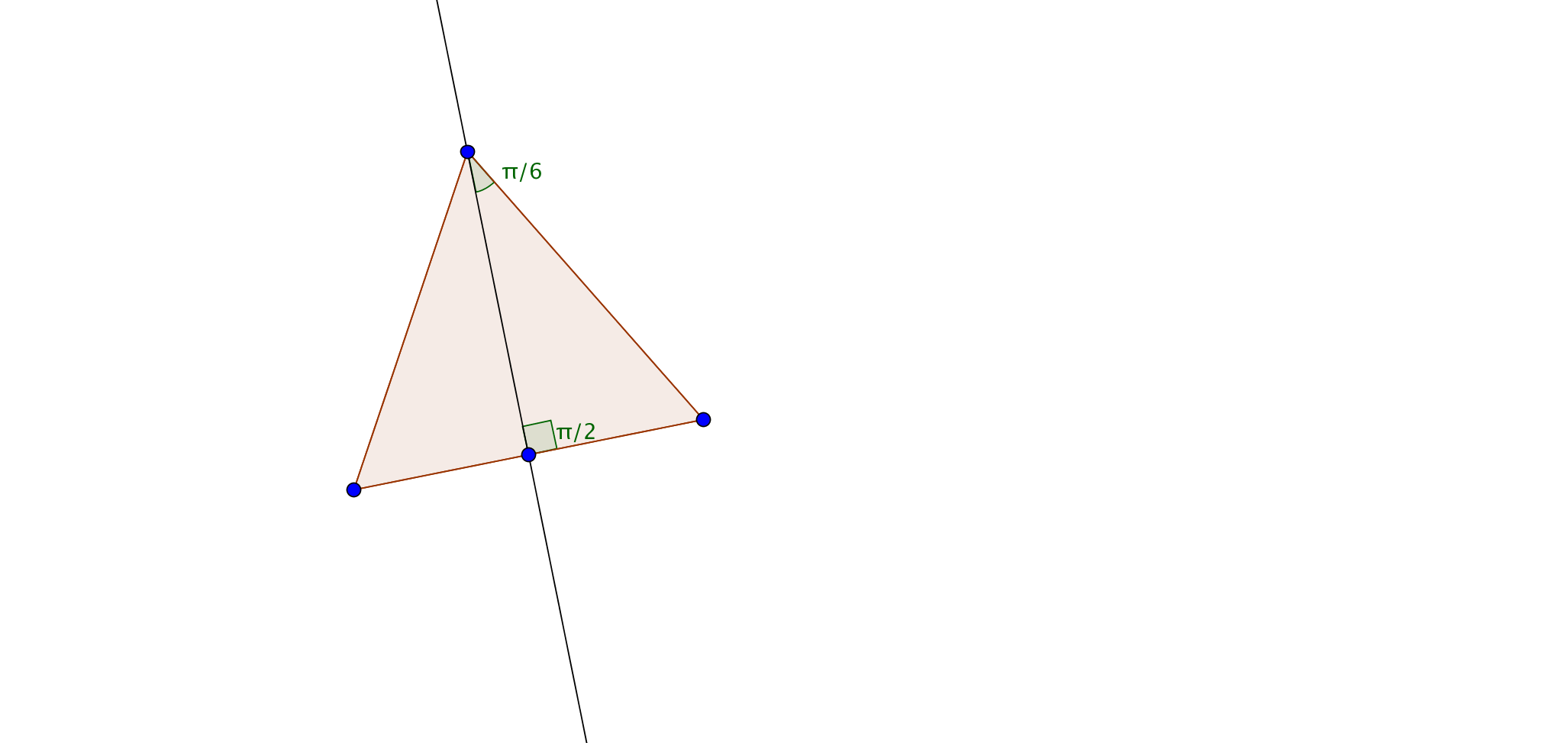
Look at the right triangle to the right. The hypotenuse is `1`. The angle marked is `pi/6`. The side opposite the angle is `1/2`. The side adjacent the angle can be found using Pythagoras' Theorem `sqrt(1^2-(1/2)^2)=sqrt(3)/2`.

Then, `sin(pi/6)=(1/2)/1=1/2` (opposite over hypotenuse); `cos(pi/6)=(sqrt(3)/2)/1=sqrt(3)/2` (adjacent over hypotenuse); `tan(pi/6)=(1/2)/(sqrt(3)/2)=1/sqrt(3)`, or `sqrt(3)/3` (opposite over adjacent).

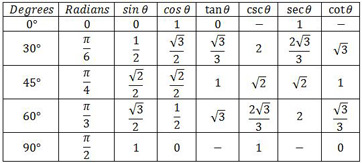
Recall the following identities (or use a unit circle):
`sin(-x)=-sin(x)` (since `sin` is an odd function)
`cos(-x)=cos(x)` (since `cos` is an even function)
`tan(-x)=-tan(x)` (since `tan` is an odd function)

Thus,
`sin(-pi/6)=-1/2`
`cos(-pi/6)=sqrt(3)/2`
`tan(-pi/6)=-1/sqrt(3)=-sqrt(3)/3`