A definite integral is an integral with upper and lower limits. The definite integral of #f(x)# is a number and it represents the area under the curve #f(x)# from #x=a# to #x=b#.
Its value is equal to #F(b)-F(a)#, where #F(x)=intf(x)dx# and this is expressed as #int_a^bf(x)dx=[F(x)]_a^b#
As #intxdx=x^2/2+c#
#int_(-2)^3xdx=[x^2/2+c]_(-2)^3#
= #[(3)^2/2+c-((-2)^2/2+c)]#
= #[9/2+c-4/2-c]#
= #5/2#
Observe that constant term #c# has cancelled out. As such we can avoid adding #c# to #F(x)#, while calculating definite integral.
Further see the following figure depicting area under the curve #f(x)=x# considered above.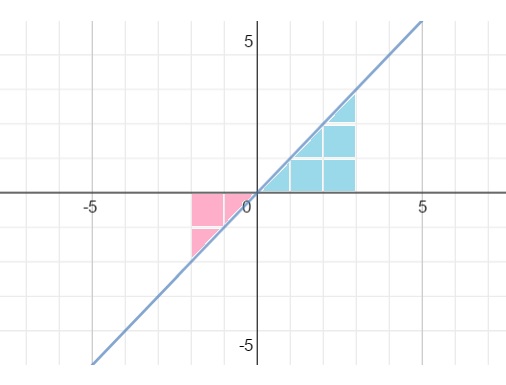
Observe that area under the #x#-axis (shown as pink in colour) has been taken as negative. If in some application of this concept, this is to be taken as positive, one must take adequate care.

