How do you evaluate the inverse function by sketching a unit circle, locating the correct angle, and evaluating the ordered pair on the circle for: tan^-1 (0)tan−1(0) and csc^-1 (2)csc−1(2)?
1 Answer
The trigonometric functions (
The inverse trigonometric functions (
Let us take a look at a unit circle diagram:
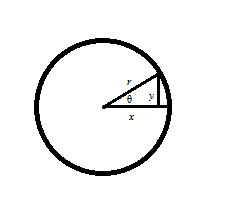 Unit circle diagram with radius
Unit circle diagram with radius
We will start with
y/x = 0yx=0 .
Clearly, this statement can only be true if
So,
arctan 0 = 0arctan0=0 .
Let us move on to
Well, the cosecant of an angle is the inverse of its sine. In other words,
csc theta = 1/sin thetacscθ=1sinθ .
We know that sine gives a ratio between the opposite side and the hypotenuse. So, the cosecant function therefore gives a ratio between the hypotenuse and the opposite side. And, if the arc-cosecant takes this ratio as an argument, and gives the angle, then we know that
2 = r/y2=ry
This is more conveniently written as:
2y = r2y=r
Or, alternatively as:
y = 1/2 ry=12r
What this tells us is that for our angle
And, elementary geometry tells us that this is precisely what occurs in a 30-60-90 triangle.
If


