Question

How do you express the solution set of the inequality in interval notation and graph the interval of `x>7/4`?

Answer 1

Please see below

Explanation:

When we are learning this, it is helpful to draw (or at least think about) the graph before we write the interval notation.

Notice that `x > 7/4` tells us that on the number line, `x` is to the right of `7/4`.

If we write this with a less than instead of a greater than, it looks like this:

`7/4 < x`.

It still says that `x` is to the right of `7/4` and now it looks that way too.

Here is my attempt at a picture:

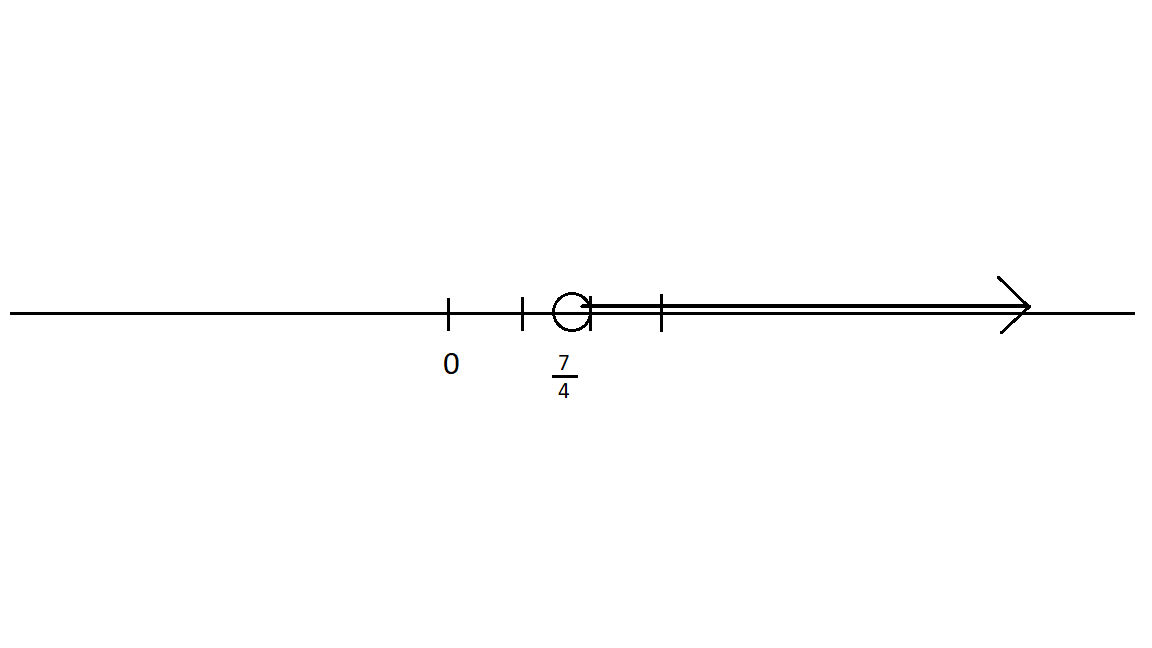
The circle at `7/4` is not filled in because the inequality is not true when `x` is equal to `7/4`.

When writing interval notation, we use a parenthesis, like this ( to show that the number I'm about to mention is not included in the interval.
(A bracket, like this [, is used to show that the number is included.)

So we know we want to start with `(7/4,`

There is no number so big that it is not in the interval. The graph has no end on the right, it just keeps going forever.

We don't want people to think we forgot to write the rest of the interval.

I guess we could just leave a blank space, like this: `(7/4,color(white)"XX")`but that's not very clear.

The convention in mathematics is to use the symbol `oo`, which we read "infinity" to indicate that there is no end of the interval on the right. We write

`(7/4,oo)`

the interval starts at `7/4`, but doesn't include `7/4` and goes to the right forever,

Because the special symbol `oo` is not a number, we never use a bracket next to it. (It does not represent a number that could be included in a set of numbers.)