How do you factor given that #f(6)=0# and #f(x)=5x^3-27x^2-17x-6#?

Question

2812 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-11T17:02:42

We know that #(x-6)# is a factor of #f(x)# because of the given root.

Using synthetic division, I divided f(x) by (x-6) to get the other factor.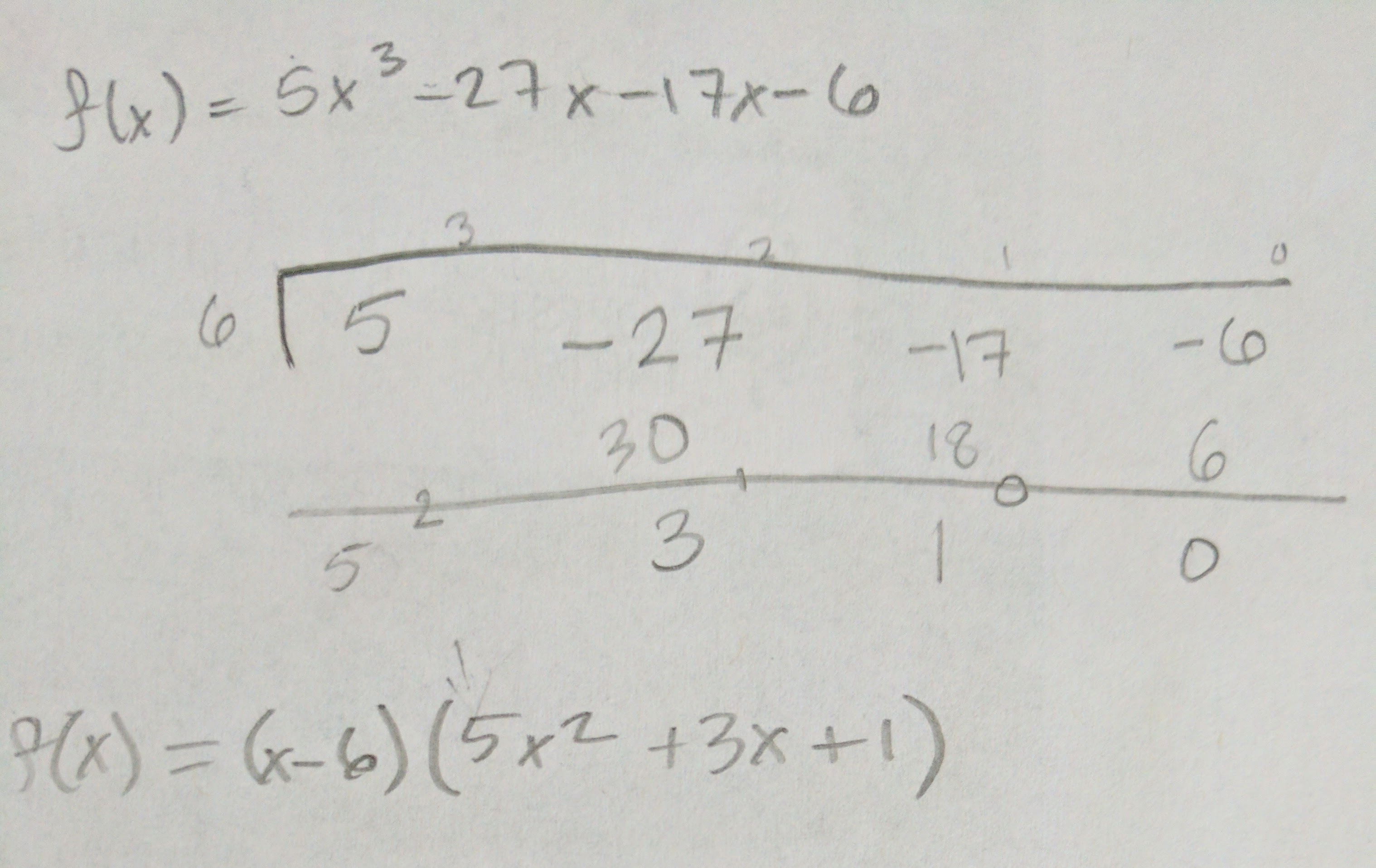 enter image source here

#f(x)=(x-6)(5x^2+3x+1)#

Answer 2 · 2016-11-11T17:15:39

The only real factor of #f(x)# are #(5x^2+3x+1)(x-6)#. However, complex factors are #5(x-6)(x+(3+isqrt11)/10)(x+(3-isqrt11)/10)#

As #f(x)=5x^3-27x-17x-6# and #f(6)=0#, #(x-6)# is a factor of #f(x)#.

Hence #f(x)=5x^3-27x^2-17x-6#

#color(white)(XXXXXx)=5x^2(x-6)+3x(x-6)+1(x-6)#

#color(white)(XXXXXx)=(5x^2+3x+1)(x-6)#

As determinant (given by #b^2-4ac#) in #5x^2+3x+1# is #3^2-4xx5xx1=-11<0#, #5x^2+3x+1# cannot be factorized further with real roots.

Hence only factor are #(5x^2+3x+1)(x-6)#.

However for #5x^2+3x+1=0#, #x=(-3+-sqrt(-11))/10#

Hence, we can have complex factors

#f(x)=5x^3-27x-17x-6#

= #5(x-6)(x+(3+isqrt11)/10)(x+(3-isqrt11)/10)#