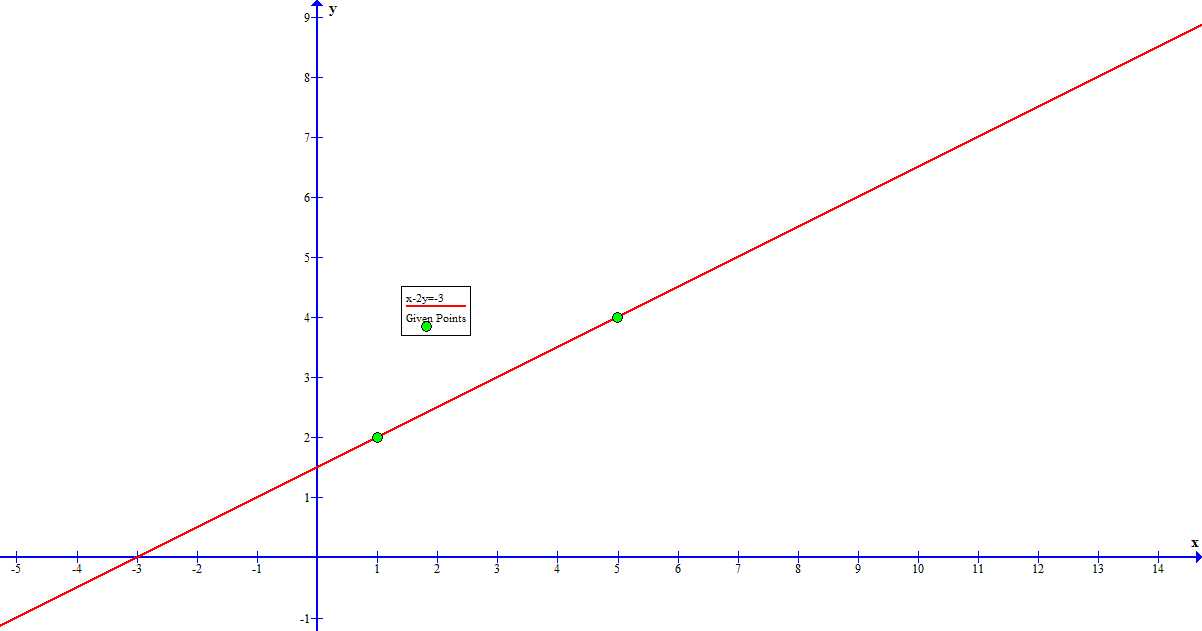
Step 1: Develop the slope-point form for the line
Given two points #(color(red)(x_1),color(blue)(y_1))# and #(x_2,y_2)#
the slope between the points is
#color(white)("XXX")color(green)m=(y_2-color(blue)(y_1))/(x_2-color(red)(x_1))#
and
the slope point form is
#color(white)("XXX")y-color(blue)(y_1)=color(green)m(x-color(red)(x_1))#
Using #(color(red)1,color(blue)2)# as #(color(red)(x_1),color(blue)(y_1))#
and #(5,4)# as #(x_2,y_2)#
We have
#color(white)("XXX")color(green)m=(4-color(blue)2)/(5-color(red)1)=color(green)(1/2)#
and the slope-point form is
#color(white)("XXX")y-color(blue)2=color(green)(1/2)(x-color(red)1)#
Step 2: convert the slope point form into standard form
Note that the standard form is
#color(white)("XXX")color(magenta)Ax+color(brown)Bx=color(purple)C#
with integer values for #color(magenta)A, color(brown)B, color(purple)C# and #color(magenta)A>=0#
Starting from the slope-point form
#color(white)("XXX")y-2=1/2(x-1)#
Multiply both sides by #2#
#color(white)("XXX")2y-4=x-1#
Subtract #x# and add #4# to both sides
#color(white)("XXX")-x+2y=3#
Multiply both sides by #(-1)# (to make the coefficient of #x# positive
#color(white)("XXX")x-2y=-3#