How do you find a polar equation that has the same graph as the given rectangular equation: #x^2# - #y^2# =1?

Question

3041 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-27T23:57:11

#r^2=sec2x#

The relation between polar coordinates #(r,theta)# and rectangular or Cartesian coordinates #(x,y)# is given by

#x=rcostheta# and #y=rsintheta#

Hence using these transformations, we can write

#x^2-y^2=1# as

#r^2cos^2x-r^2sin^2x=1#

or #r^2(cos^2x-sin^2x)=1#

or #r^2cos2x=1# or #r^2=sec2x#

The graph of the equation representing a hyperbola appears as

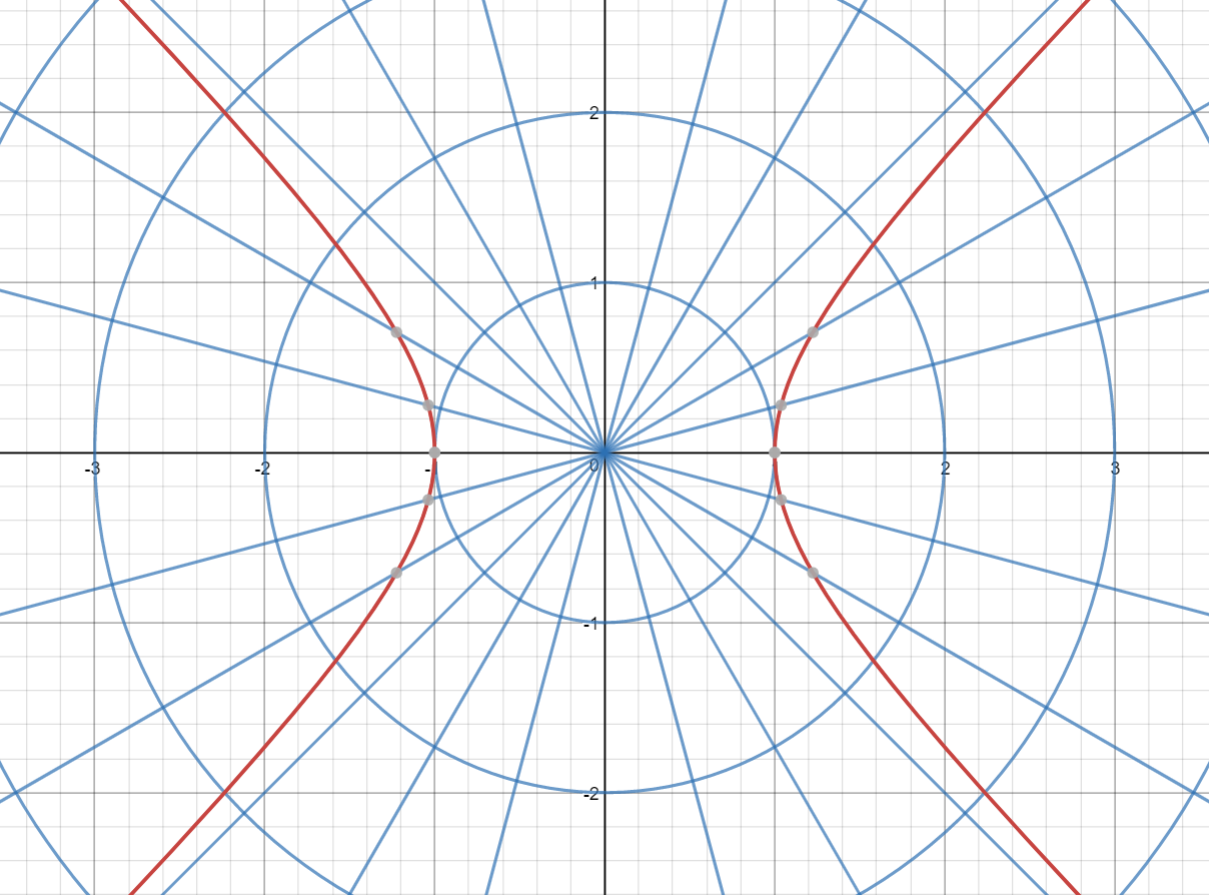prepared using utility at desmos.com