How do you find a polynomial f(x) of degree 3 with real coefficients and the following zeros 1, 3-i?

Question

12869 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-11-18T19:21:58

Since complex roots ALWAYS occur in conjugate pairs ...

#f(x) = (x-1)[x-(3-i)][x - (3+i)]#

Next, simplify ...

#f(x)=(x-1)(x^2-6x+10)#

#=x^3-7x^2+16x-10#

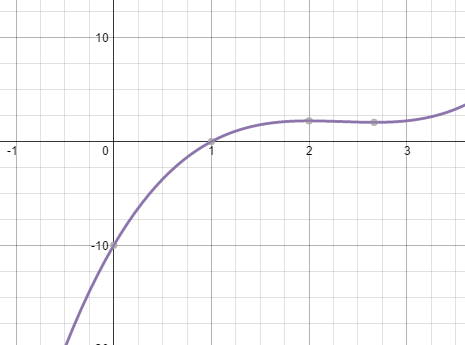
From the graph below, the function is a cubic with only one real root (at #x=1#) and two imaginary roots .

hope that helped

enter image source here