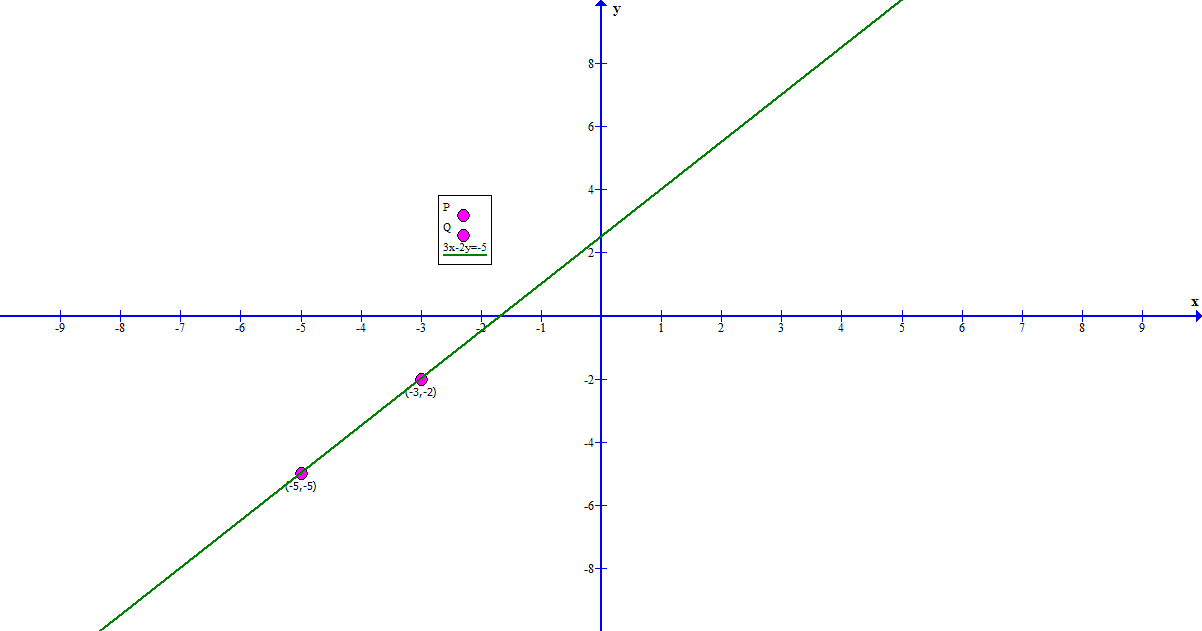Question

How do you find a standard form equation for the line with P= (-5,-5) and Q= (-3,-2)?

Answer 1

`3x-2y=-5`
(see below for method)

Explanation:

Step 1: Develop a slope-point form for the line
The slope of a line between two points is defined as:
`color(white)("XX")`The difference between the `y` coordinate values
`color(white)("XX")`divided by the corresponding difference between the `x` coordinates.
`color(white)("XXXXX")m=(Deltay)/(Deltax)= (-2-(-5))/(-3-(-5))=3/2`

This relationship must hold for any arbitrary point `(x,y)` on the line;
so
`color(white)("XXXXX")m=(y-(-5))/(x-(-5))=(y+5)/(x+5)`

Therefore
`color(white)("XXXXX")(y+5)/(x+5)=3/2`
or
`color(white)("XXXXX")y+5 =3/2(x+5)`

Step 2: Convert the slope-point form into standard form
Note that the standard form for a linear equation is
`color(white)("XX")Ax+By=C` with constants `A, B, C` and `A>=0`

If
`color(white)("XXXXX")y+5=3/2(x+5)`
then
`color(white)("XXXXX")2(y+5)=3(x+5)`
`rArr`
`color(white)("XXXXX")2y+10=3x+15`
`rArr`
`color(white)("XXXXX")-5=3x-2y`
or
`color(white)("XXXXX")3x-2y=-5`

Here is the graph for verification purposes: