Question

How do you find all points on the curve `x^2 + xy + y^2 = 7` where the tangent line is parallel to the x-axis, and the point where the tangent line is parallel to the y-axis?

Answer 1

The tangent line is parallel to the `x` axis when the slope (hence `dy/dx`) is zero and it is parallel to the `y` axis when the slope (again, `dy/dx`) goes to `oo` or `-oo`

Explanation:

We'll start by finding `dy/dx`:

`x^2 + xy + y^2 = 7`

`d/dx(x^2 + xy + y^2) = d/dx(7)`

`2x + 1y +xdy/dx + 2y dy/dx = 0`

`dy/dx = - (2x+y)/(x+2y)`

Now, `dy/dx = 0` when the nuimerator is `0`, provided that this does not also make the denominator `0`.

`2x+y=0` when `y = -2x`

We have now, two equations:
`x^2 + xy + y^2 = 7`
`y = -2x`

Solve (by substitution)

`x^2 + x(-2x) + (-2x)^2 = 7`

`x^2 -2x^2+4x^2 = 7`

`3x^2 =7`

`x = +- sqrt(7/3) = +- sqrt21/3`

Using `y = -2x`, we get
The tangent to the curve is horizontal at the two points:

`(sqrt21/3, -(2sqrt21)/3)` and `(-sqrt21/3, (2sqrt21)/3)`

(Observe that these pair do not also make the denominator of `dy/dx` equal to `0`)

To find the points at which the tangent is vertical, make the denominator of `dy/dx` equal tpo `0` (without also making the numerator `0`).

We could go through the solution, but the symmetry of the equation that we will get:

`x=-2y`, so

`y = +- sqrt21/3`

and the points on the curve at which the tangent is vertical are:

`(-(2sqrt21)/3, sqrt21/3)` and `((2sqrt21)/3, -sqrt21/3)`

By the way. Because we do have the technology, here is the graph of this rotated ellipse: (Note that `+-sqrt21/3 ~~ +- 1.528` which you can see on the graph.)

graph{x^2 + xy +y^2 =7 [-11.3, 11.2, -5.665, 5.585]}

Answer 2

Using only middle school math I get

Tangents parallel to the x axis at:

`(-sqrt{7/3}, 2sqrt{7/3}) and (sqrt{7/3}, -2sqrt{7/3})`

Tangents parallel to the y axis at:

`(-2sqrt{7/3}, sqrt{7/3}) and (2sqrt{7/3}, -sqrt{7/3})`

Explanation:

I glanced at Jim's answer, which looks like a nice, standard calculus treatment. But I couldn't help but feel sad for all the middle schoolers out there in Socratic land who want to find tangents of algebraic curves but are still years away from calculus.

Fortunately they can do these problems using only Algebra I.

`x^2+xy+y^2=7`

This might be a bit complicated for a first example, but let's go with it. We write our curve as `f(x,y)=0` where

`f(x,y) = x^2+xy+y^2-7`

Let's take `(r,s)` as a point on `f`. We want to investigate `f` near `(r,s)` so we write

`f(x,y)=f(r + (x-r), s + (y-s))`

`= (r + (x-r)) ^2+(r + (x-r))( s + (y-s))+( s + (y-s))^2-7`

We expand, but we don't expand the difference terms `x-r` and `y-s`. We want to keep those intact so we can experiment with eliminating some later.

`f(x,y) = r^2 + 2r(x-r) + (x-r) ^2+ (rs + s(x-r) + r(y-s) + (x-r)(y-s))+s^2 + 2s(y-s) + (y-s)^2-7`

`= ( r^2 + rs + s^2 - 7) + (2r+s)(x-r) + (2s+r)(y-s) + (x-r) ^2+ (y-s)^2+ (x-r)(y-s)`

`= f(r,s) + (2r+s)(x-r) + (2s+r)(y-s) + (x-r) ^2+ (y-s)^2+ (x-r)(y-s)`

We said `(r,s)` is on `f` so `f(r,s)=0`.

`f(x,y) = (2r+s)(x-r) + (2s+r)(y-s) + (x-r) ^2+ (y-s)^2+ (x-r)(y-s)`

We sorted the terms by degree, and we can experiment with approximations to `f` near `(r,s)` by dropping the higher degrees. The idea is when `(x,y)` is near `(r,s)` then `x-r` and `y-s` are small, and their squares and product are smaller still.

Let's just generate some approximations to `f`. Since `(r,s)` is on the curve, the constant approximation, dropping all the difference terms, is

`f_0(x,y) = 0`

That's not particularly exciting, but it correctly tells us points near `(r,s)` will give a value near zero for `f`.

Let's get more interesting and keep the linear terms.

`f_1(x,y) = (2r+s)(x-r) + (2s+r)(y-s)`

When we set this to zero, we get the best linear approximation to `f` near `(r,s),` which is the tangent line to `f` at `(r,s).` Now we're getting somewhere.

`0 = (2r+s)(x-r) + (2s+r)(y-s)`

We can consider other approximations as well:

`f_2(x,y) = (2r+s)(x-r) + (2s+r)(y-s) + (x-r) ^2`

`f_3(x,y) = (2r+s)(x-r) + (2s+r)(y-s) + (x-r) ^2 + (x-r)(y-s)`

These are higher order tangents, ones that college math students hardly ever get to. We've already gone beyond college calculus.

There are more approximations, but I'm being warned this is getting long. Now that we learned how to do calculus using only Algebra I, let's do the problem.

We want to find the points where the tangent line is parallel to the `x` axis and `y` axis.

We found our tangent line at `(r,s)` is

`0 = (2r+s)(x-r) + (2s+r)(y-s)`

Parallel to the `x` axis means an equation `y = text{constant}`. So the coefficient on `x` must be zero:

`2r + s = 0`

`s = -2r`

`(r,s)` is on the curve so `f(r,s)=0`:

`r^2 + rs + s^2 - 7 = 0`

`r^2 + r(-2r) + (-2r)^2 - 7 = 0`

`r =pm sqrt{7/3}`

Since `s=-2r` the points are

`(-sqrt{7/3}, 2sqrt{7/3}) and (sqrt{7/3}, -2sqrt{7/3})`

Similarly parallel to the y axis means `2s+r=0` which should just swap x and y due to the symmetry of the problem. So the other points are

`(-2sqrt{7/3}, sqrt{7/3}) and (2sqrt{7/3}, -sqrt{7/3})`

Check.

How to check? Let's do an Alpha plot .

plot x^2+xy+y^2=7, x=-sqrt{7/3}, y=2 sqrt{7/3}, x=2sqrt{7/3}, y =-sqrt{7/3}

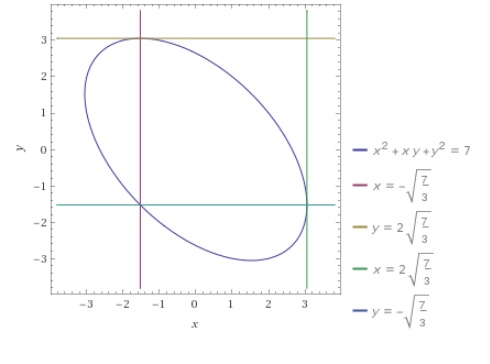
Looks good. Calculus on algebraic curves. Pretty good for middle school.