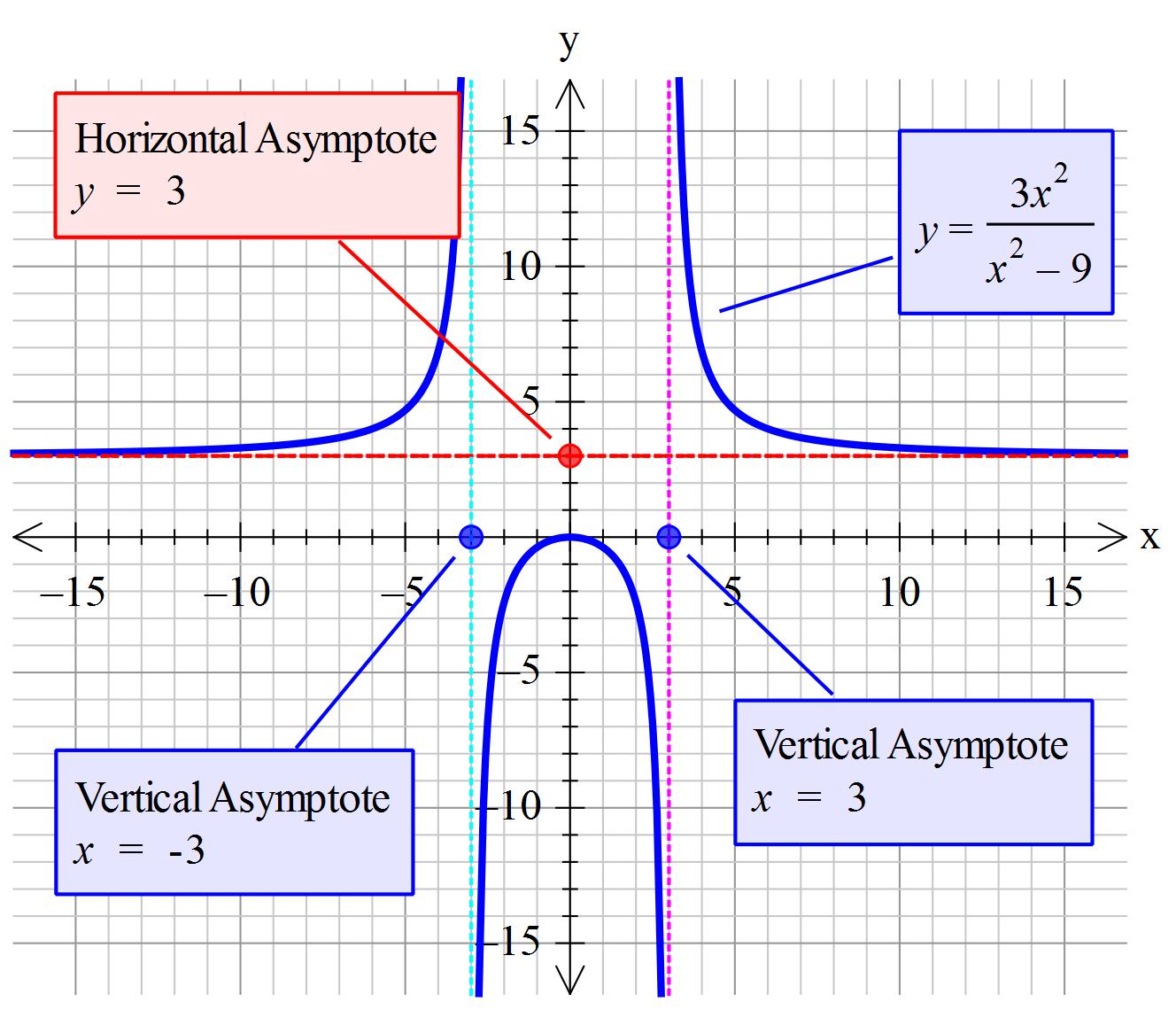
Write as #y=(3x^2)/(x^2(1-9/x^2)) = 3/(1-9/x^2)#
#color(blue)("Determine horizontal asymptote")#
As #x# becomes increasingly large then #9/x^2# becomes increasingly small.
#color(blue)(y=lim_(x->+-oo) 3/(1-9/x^2) ->3/1 larr "horizontal asymptote")#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine vertical asymptote")#
#color(brown)("As "x^2" gets closer and closer to 9 then "1-9/x^2" becomes ")##color(brown)("smaller and smaller. So "3/(1-9/x^2)" becomes larger and larger.")#
#" "y=lim_(x->3) 3/(1-9/x^2)->oo#
#color(brown)("However; if "x=color(white)()^+3" then "9/(color(white)()^+3)<1 #
#" "y=lim_(x->color(white)()^+3) 3/(1-9/x^2)->+oo#
#color(brown)("However; if "x=color(white)()^-3" then "9/(color(white)()^+3)>1 #
#" "y=lim_(x->color(white)()^+3) 3/(1-9/x^2)->-oo#
So #color(blue)(y=lim_(x->3) 3/(1-9/x^2)->+-oo larr " vertical asymptotes")#