Question

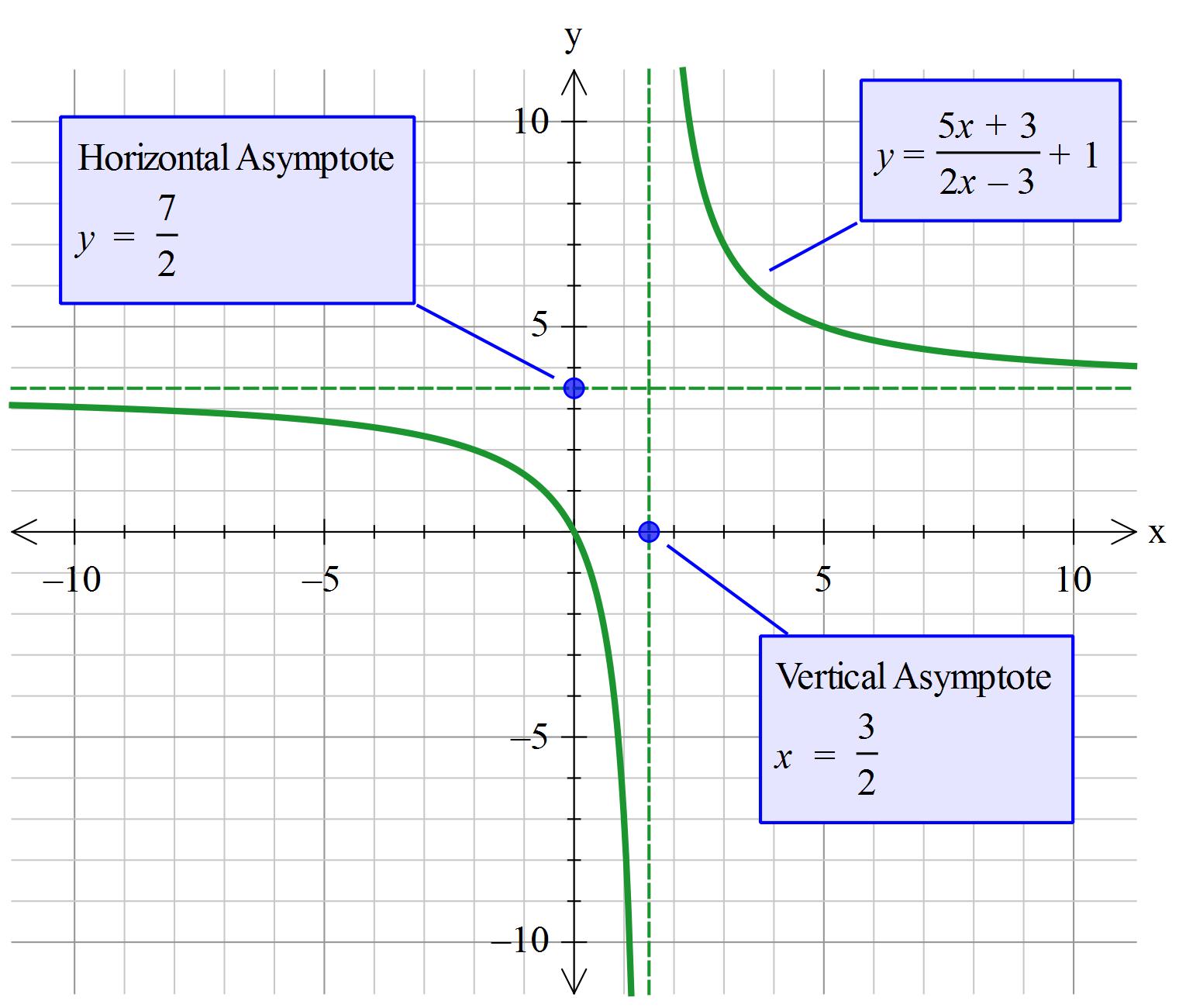
How do you find all the asymptotes for function `f(x)=[(5x+3)/(2x-3)]+1`?

Answer 1

`color(green)("Horizontal asymptote at "y=5/2)`

`color(green)("Vertical asymptote at "x=3/2)`

Explanation:

The objective of this type of question is to make you think about what an equation is actually doing or saying about a situation.

Asymptotes are where the equation is getting very close to a value that is undefined or a value that does indeed exists but only as `x="infinity or zero"` is approached.

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
There are two things to bear in mind with your question.

`color(brown)("Point 1.")` It contains a fraction. Thus the denominator is undefined
`color(white)(...........)`(not allowed) to become zero.

`color(brown)("Point 2.")" It will have a specific value that it tends to as "x` `color(white)(.............)" becomes enormously large"`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Consider point 1")`

`2x-3=0 => x=3/2`

`color(green)("Vertical asymptote at "x=3/2)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Consider point 2")`

As `x` becomes extremely large the equation will behave as if it is `(5/2xx x/x)+1" " =" " (5/2xx1)+1" " = " "7/2`

`color(green)("Horizontal asymptote at "y=5/2)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~