How do you find all the real and complex roots of #x^5 + 7x^3 + 3x + 2 = 0#?

Question

1472 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-06-04T14:13:00

Use a numerical method to find approximations for the roots:

#x ~~ -0.44915#

#x ~~ 0.249655+-0.786034i#

#x ~~ -0.0250794+-2.55851i#

#f(x) = x^5+7x^3+3x+2#

In common with quintics in general, this quintic has no zeros expressible in algebraic terms using #n#th roots.

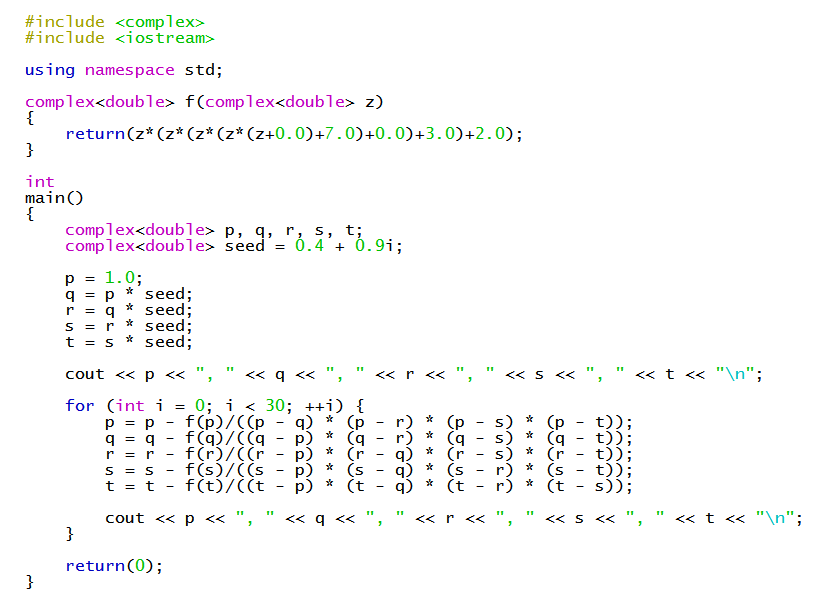
We can find numerical approximations for the zeros using a method such as Durand-Kerner.

For another quintic solution approximated using Durand-Kerner, see https://socratic.org/s/av3SsZ5D

In the current example we find approximations:

#x ~~ -0.44915#

#x ~~ 0.249655+-0.786034i#

#x ~~ -0.0250794+-2.55851i#

I used this C++ program:

enter image source here

How do you find all the real and complex roots of #x^5 + 7*x^3 + 3*x + 2 = 0#?