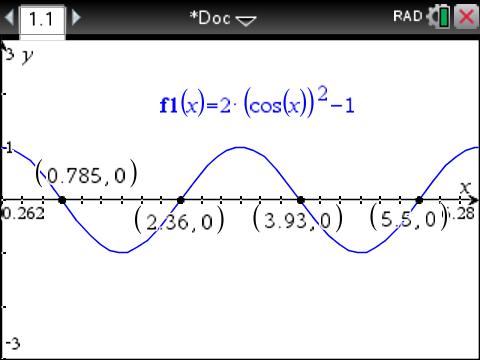
How do you find all the solutions in the interval [0, 2pi): #2 cos^2(2x) - 1 = 0#?
1 Answer
Mar 28, 2016
Isolate the angle 2x, by following the reverse "order of operations".
Explanation:
Step 1: Add 1 to both sides:
Step 2: Divide both sides by 2:
Step 3: Take the square root of both sides:
(don't forget the positive and negative solutions!)
Step 4: Use inverse of cosine to find the angles:
Step 5: Find angles that work:
Step 6: Solve for x:
(decimal approximations are seen on the graph below)