How do you find all the zeros of # f(x)=2x^3-13x^2+22x-8#?
1 Answer
Apr 1, 2016
Use the Rational Factor Theorem to identify rational zeros.
Explanation:
According to the Rational Factor Theorem
if
they must be in the set
Evaluating the equation for each possibility:
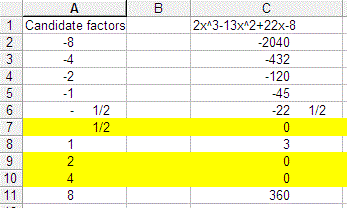
identifies the zeros as#{color(red)(1/2),color(blue)(2),color(brown)(4)}#
which implies the factoring:
#color(white)("XXX")(color(red)(2x-1))(color(blue)(x-2))(color(brown)(x-4))#
