How do you find all the zeros of #f(x) = 9x^4 – 17x^3 + 2x^2 – 3x + 33#?
1 Answer
Check that it has no rational zeros, then resort to a numerical method to find approximations.
Explanation:
By the rational root theorem, any rational zeros of
So the only possible rational zeros are:
#+-1/9# ,#+-1/3# ,#+-1# ,#+-11/9# ,#+-3# ,#+-11/3# ,#+-11# ,#+-33#
In addition, notice that if you invert the signs of the coefficients on the terms of odd degree, then all of the resulting coefficients are positive. Hence
So the only possible rational zeros are:
#1/9, 1/3, 1, 11/9, 3, 11/3, 11, 33#
We find that
It is possible to solve such a quartic algebraically, but it gets very messy and is not necessarily very useful.
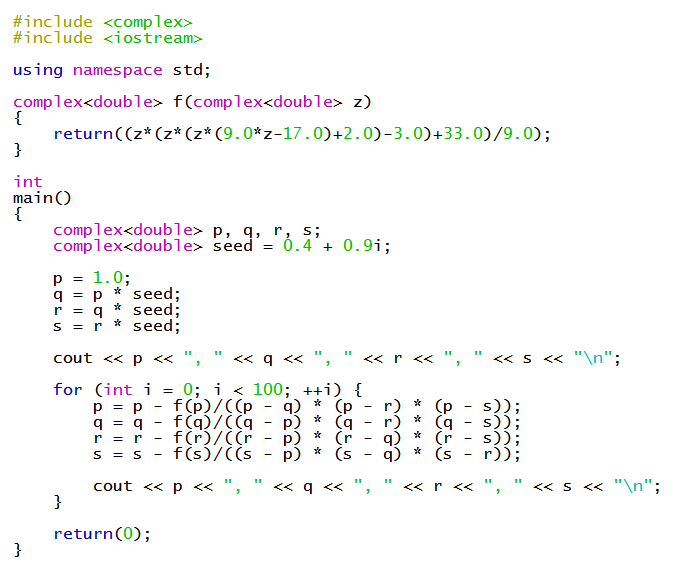
You can use a numerical method such as Durand-Kerner to find good approximations to the two pairs of Complex zeros that it does have.
See https://socratic.org/s/av2PtWLY for an example finding approximations for the zeros of a quintic.
In our example, we find approximations:
#x = 1.57163 +-0.656656i#
#x = -0.627188 +-0.932989i#
An example C++ program that performs the calculations would be: