How do you find all the zeros of #f(x)=x^5+3x^3-x+6#?

1 Answer
George C.
Jun 22, 2016

Find there are no rational zeros.

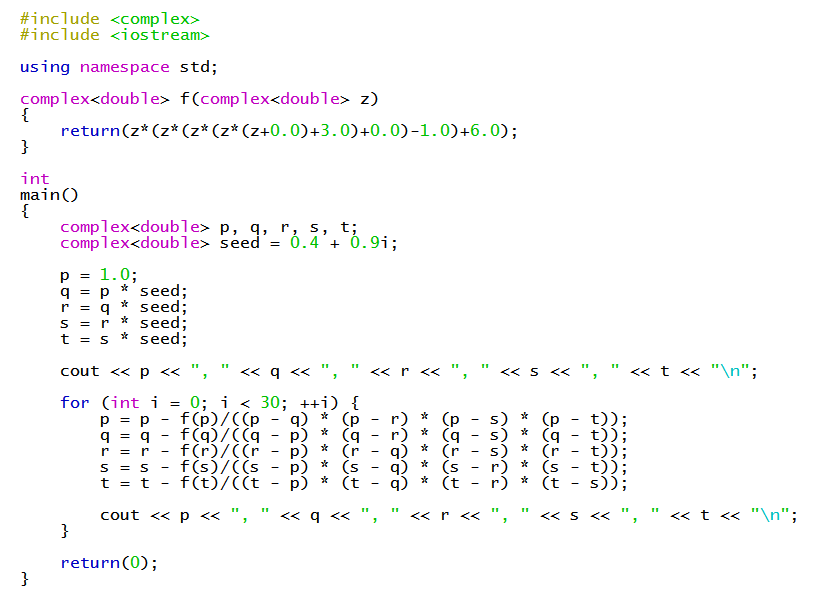
Use Durand-Kerner or similar to find approximations.

Explanation:

#f(x) = x^5+3x^3-x+6#

By the rational root theorem any rational zeros of #f(x)# are expressible in the form #p/q# for integers #p, q# with #p# a divisor of the constant term #6# and #q# a divisor of the coefficient #1# of the leading term.

That means that the only possible rational zeros are:

#+-1#, #+-2#, #+-3#, #+-6#

None of these work, so #f(x)# has no rational zeros.

In common with most quintic polynomials, the zeros are not expressible in terms of #n#th roots, so you are left with numerical methods such as Durand-Kerner to help find approximations:

#x ~~ -1.17826#

#x ~~ -0.202554+-1.89313i#

#x ~~ 0.791684+-0.882051i#

See https://socratic.org/s/avxUUEiJ for another example.

Here's a sample C++ program that implements the Durand-Kerner algorithm for this example:

enter image source here

Related questions
See all questions in Zeros
Impact of this question
2173 views around the world
You can reuse this answer
Creative Commons License