Question

How do you find all the zeros of `x^5 - 3x^4 + 5x^3 + 9x^2 + x - 2`?

Answer 1

Use a numerical method to find approximations:

`x_1 ~~ 0.390503`

`x_(2,3) ~~ 2.01006+-2.24677i`

`x_(4,5) ~~ -0.705308+-0.257059i`

Explanation:

`f(x) = x^5-3x^4+5x^3+9x^2+x-2`

By the rational root theorem, any rational zeros of `f(x)` are expressible in the form `p/q` for integers `p, q` with `p` a divisor of the constant term `-2` and `q` a divisor of the coefficient `1` of the leading term.

So the only possible rational zeros are:

`+-1`, `+-2`

Neither of these is a zero, so `f(x)` has no rational zeros.

In common with quintics in general, this `f(x)` has no algebraic solution in terms of `n`th roots.

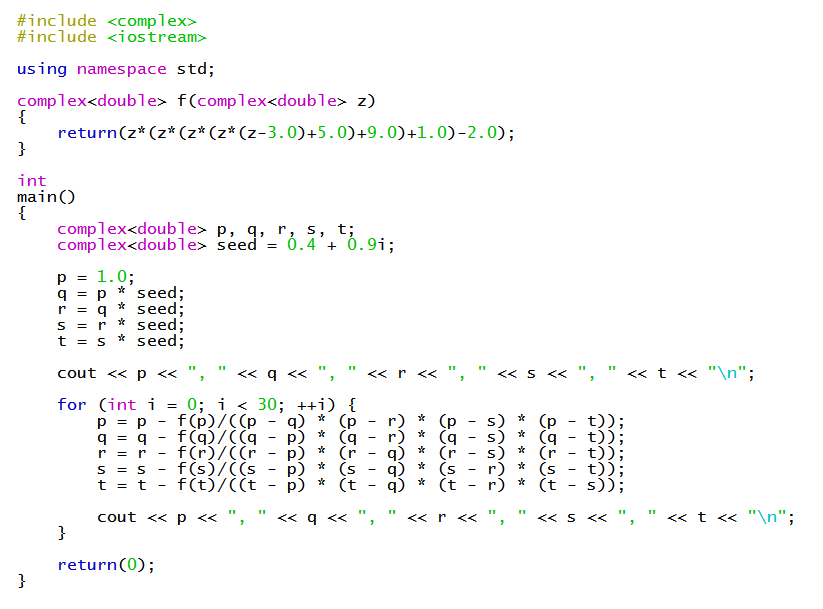
We can find rational approximations using a numeric method such as Durand-Kerner. For another example of such a quintic solution, see: https://socratic.org/s/avdSNDdg

In the current example we find approximations:

`x_1 ~~ 0.390503`

`x_(2,3) ~~ 2.01006+-2.24677i`

`x_(4,5) ~~ -0.705308+-0.257059i`

I used the following C++ program: