Question

How do you find all zeros of the function `2x^3-3x^2-16x+10`?

Answer 1

I will graph this as a function, 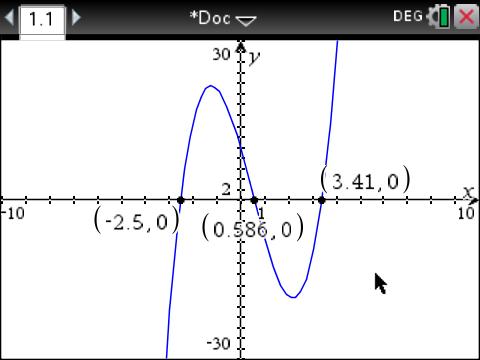`f(x) = 2x^3-3x^2-16x+10`.

Explanation:

Notice that -2.5 seems to be the "nicest" zero. That means 2x+5 is a factor. If you do long division on the original polynomial by 2x+5, you will get `x^2-4x+2`. You can solve that quadratic with the quadratic formula to get: `2+sqrt(2), 2-sqrt(2)`.