Question

How do you find an equation for the line tangent to the circle `x^2+ y^2 =25` at the point (3, -4)?

Answer 1

`y = 3/4x-25/4`

Explanation:

We could use calculus but first as with all Mathematical problems one should step back and think about what the question is asking you, and in this case we can easily answer the question using knowledge of the equation, in this case:

`x^2 + y^2 = 25`

represents a circle of centre `(a,b)=(0,0)` and radius `r=5`

First verify that `(3,-4)` actually lies on the circle;
Subs `x=3` oito the circle equation:

`=> 3^2+y^2=25 = y^2=16 => y=+- 4`

So `(3,-4)` does indeed lie on the circle. A straight line passing between that point and the centre of the circle `(0,0)` will be perpendicular to the tangent. So the gradient of the normal is given by:

`m_N = (Delta y) / (Delta x) = (-4 - 0)/(3 - 0) = -4/3`

Then as the normal is perpendicular to the tangent the product of their gradients is `-1`, so then:

`m_T = 3/4`

So using the point/slope form `y-y_1=m(x-x_1)` the equation we seek is;

`y-(-4) = 3/4(x-3)`
`:. y+4 \ \ \ = 3/4x-9/4`
`:. " " y = 3/4x-25/4`

We can confirm this solution is correct graphically:

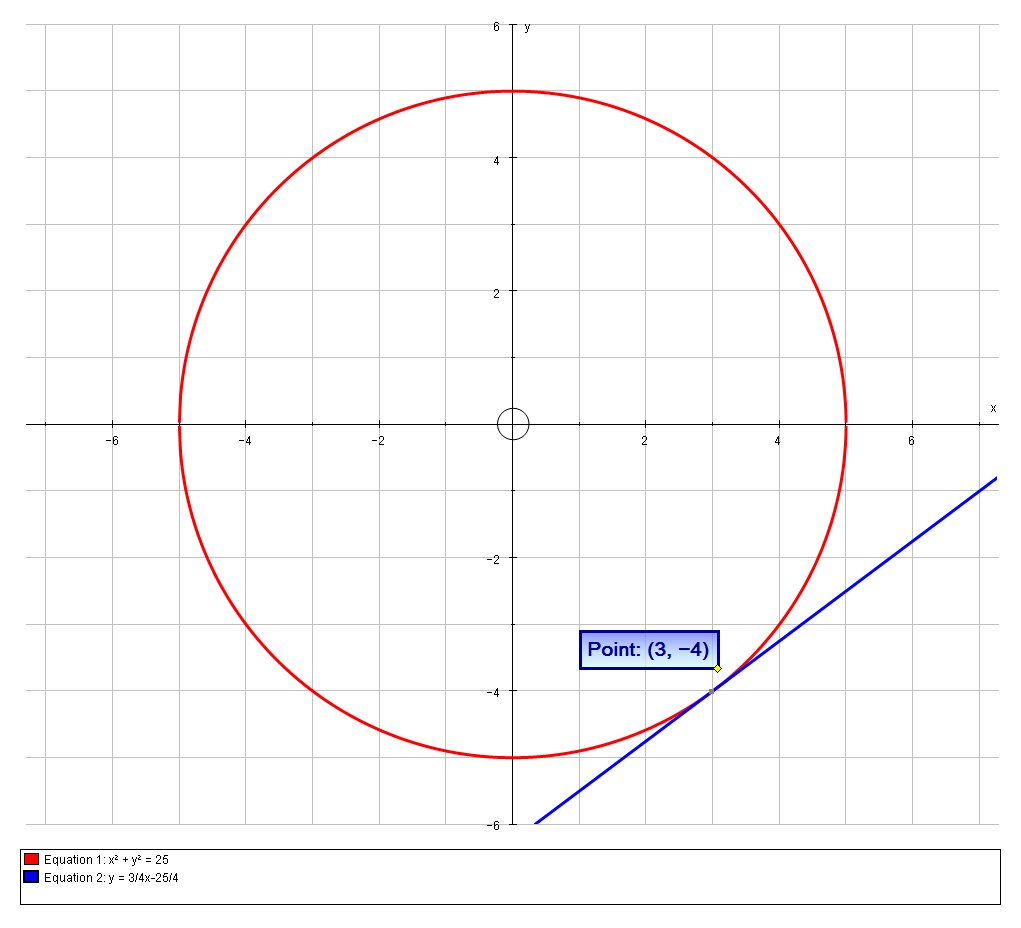
Here is the calculus solution:

If `x^2+y^2=25` then differentiating wrt `x` implicitly gives us:

`2x+2ydy/dx=0`
`:. " " dy/dx=-x/y`

When `x=3 and y=-4 => dy/dx=-3/(-4) = 3/4`, which is what we obtained above.