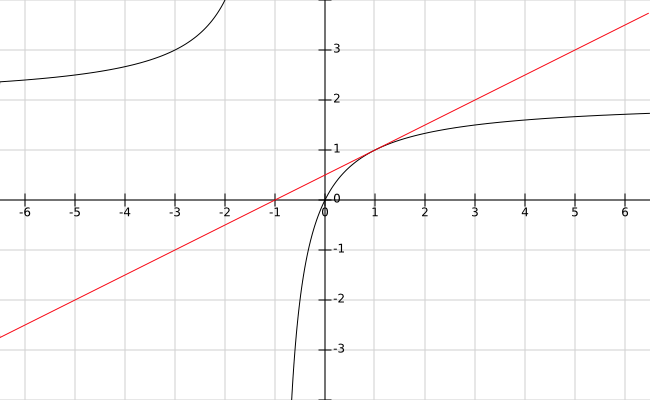
How do you find an equation of the tangent line to the curve #y=(2x)/(x+1)# at the point (1,1)?

Question

12262 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-05T04:04:52

#y=1/2x+1/2#

The equation of the line tangent to the curve #y=f(x)# in the point #(x_0, f(x_0))# is given by:

#y = f(x_0)+f'(x_0)(x-x_0)#

In our case:

#x_0 = 1#

#f(x_0) = (2*1)/(1+1) =2/2 =1#

#f'(x) = (2(x+1)-2x)/(x+1)^2 = (2x+2-2x)/(x+1)^2 =2/(x+1)^2#

#f'(x_0)= 2/(1+1)^2 = 2/2^2 = 2/4 = 1/2#

So the equation of the tangent line is:

#y = 1+1/2(x-1) = 1+1/2x-1/2 =1/2x +1/2#

enter image source here