Given
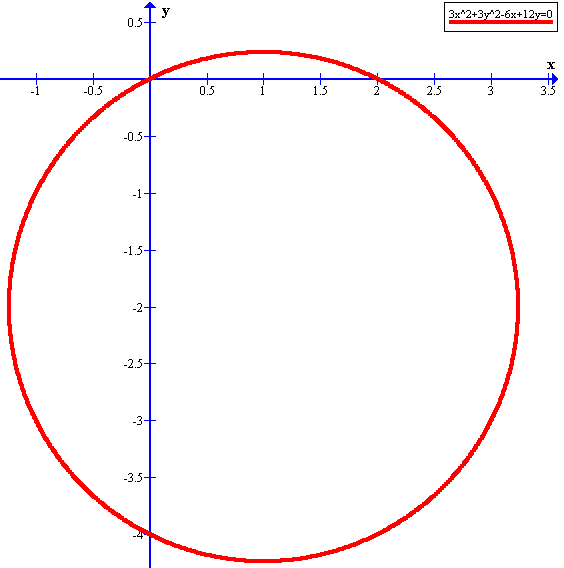
#color(white)("XXX")3x^2+3y^2-6x+12y=0#
Let's start by simplifying by dividing everything by the common factor of #3#
#color(white)("XXX")x^2+y^2-2x+4y=0#
Our target will be to convert this into standard circle form:
#color(white)("XXX")(x-color(red)a)^2+(y-color(blue)b)^2=color(green)r^2#
for a circle with center #(color(red)a,color(blue)b)# and radius #color(green)r#
Regrouping the #x# and #y# terms separately
#color(white)("XXX")(x^2-2xcolor(white)("XX"))+(y^2+4ycolor(white)("XX"))=0#
Completing the square for each
#color(white)("XXX")(x^2-2xcolor(cyan)(+1))+(y^2+4ycolor(purple)(+4))=0color(cyan)(+1)color(purple)(+4)#
Rewriting as squares in standard circle form
#color(white)("XXX")(x-color(red)1)^2+(y-color(blue)(""(-2)))^2=color(green)(""(sqrt(5))^2#
This gives us
#color(white)("XXX")#Center at #(color(red)1,color(blue)(-2))#
#color(white)("XXX")#Radius of #color(green)(sqrt(5))#
To get the intercepts, it is probably easier to work from the earlier equation:
#color(white)("XXX")x^2+y^2-2x+4y=0#
The Y-intercepts occur when #x=0#
#color(white)("XXX")y^2+4y=0#
#color(white)("XXX")y(y+4)=0
#color(white)("XXX")y=0 or y=--4#
The X-intercepts occur when #y=0#
#color(white)("XXX")x^2-2x=0#
#color(white)("XXX")x(x-2)=0#
#color(white)("XXX")x=0 or x=2#