Again, let #f# be defined in a piecewise way by #f(x)=x^2sin(1/x)# when #x!=0# and #f(0)=0#.
Certainly, when #x!=0# the function is differentiable and continuous and the Product Rule and Chain Rule can be used to say that:
#f'(x)=2x*sin(1/x)+x^2*cos(1/x)*(-1)x^{-2}#
#=2xsin(1/x)-cos(1/x)# for #x!=0#.
But #f# is continuous everywhere (#lim_{x->0}f(x)=0=f(0)# by the Squeeze Theorem) and #f'(0)# happens to exist as well! Do a limit calculation:
#f'(0)=lim_{h->0}(f(0+h)-f(0))/h=lim_{h->0}(h^2*sin(1/h)-0)/h#
#=lim_{h->0}hsin(1/h)=0#, where the last equality follows by the Squeeze Theorem.
In other words, #f'(0)=0#.
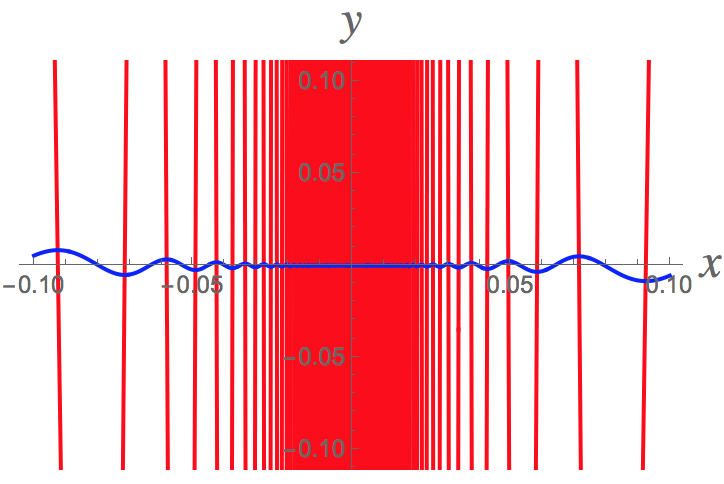
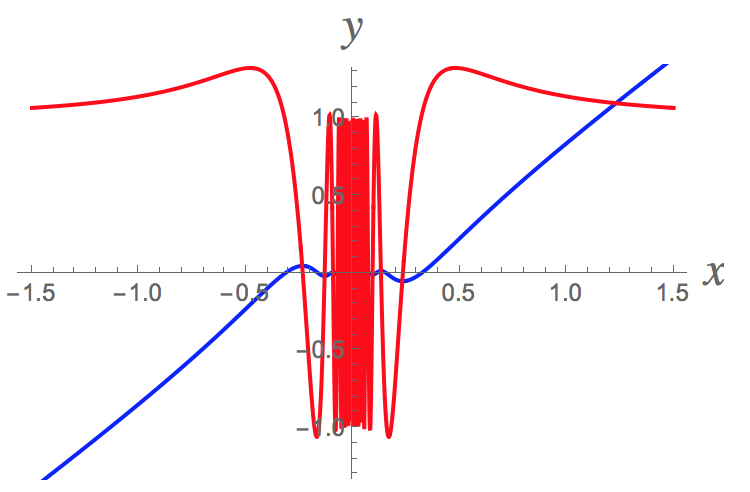
Here's a graph of the function #f# (blue) and its derivative #f'# (red). Even though the derivative exists everywhere, it is not well-behaved near the origin. Not only does it have infinitely many oscillations as #x->0#, but the oscillations never decrease below 1 in amplitude (and #lim_{x->0}f'(x)# fails to exist so that #f'# is not continuous at #x=0#). On the other hand, the graph of the derivative contains the point #(0,0)# as well.
Pretty amazing, isn't it?!?!
Here a closer view near the origin and also making sure we can still see the blue curve. It's oscillating infinitely often as #x->0# as well, though the oscillations are rapidly decreasing in amplitude as #x->0#.