How do you find #\lim _ { x \rightarrow \infty } ( \frac { 5x + 9} { 7x ^ { 2} - 2x + 1} )#?
3 Answers
Explanation:
if the denominator is a higher degree polynomial than the numerator (
you can also check the value of
as x approaches
you can also confirm with the graph: graph{(5x+9)/(7x^2-2x+1) [-10.15, 18.32, -6.84, 7.4]}
0
Explanation:
You can think about this in a couple of ways.
First, look at the polynomials in the numerator and denominator: which one is increasing faster?
The one in the denominator is, right? It's a 2nd degree polynomial, while the one in the numerator is 1st degree.
Hence, as
If you prefer seeing this more algebraically, then we can use the method of dividing every term by the highest power in the expression. In this case, we have
You can now take the limit of each term in this expression.
Now, notice that you have a lot of terms where a constant is being divided by
Hope that helped :)
Approach for exam use ....
:-)
Explanation:
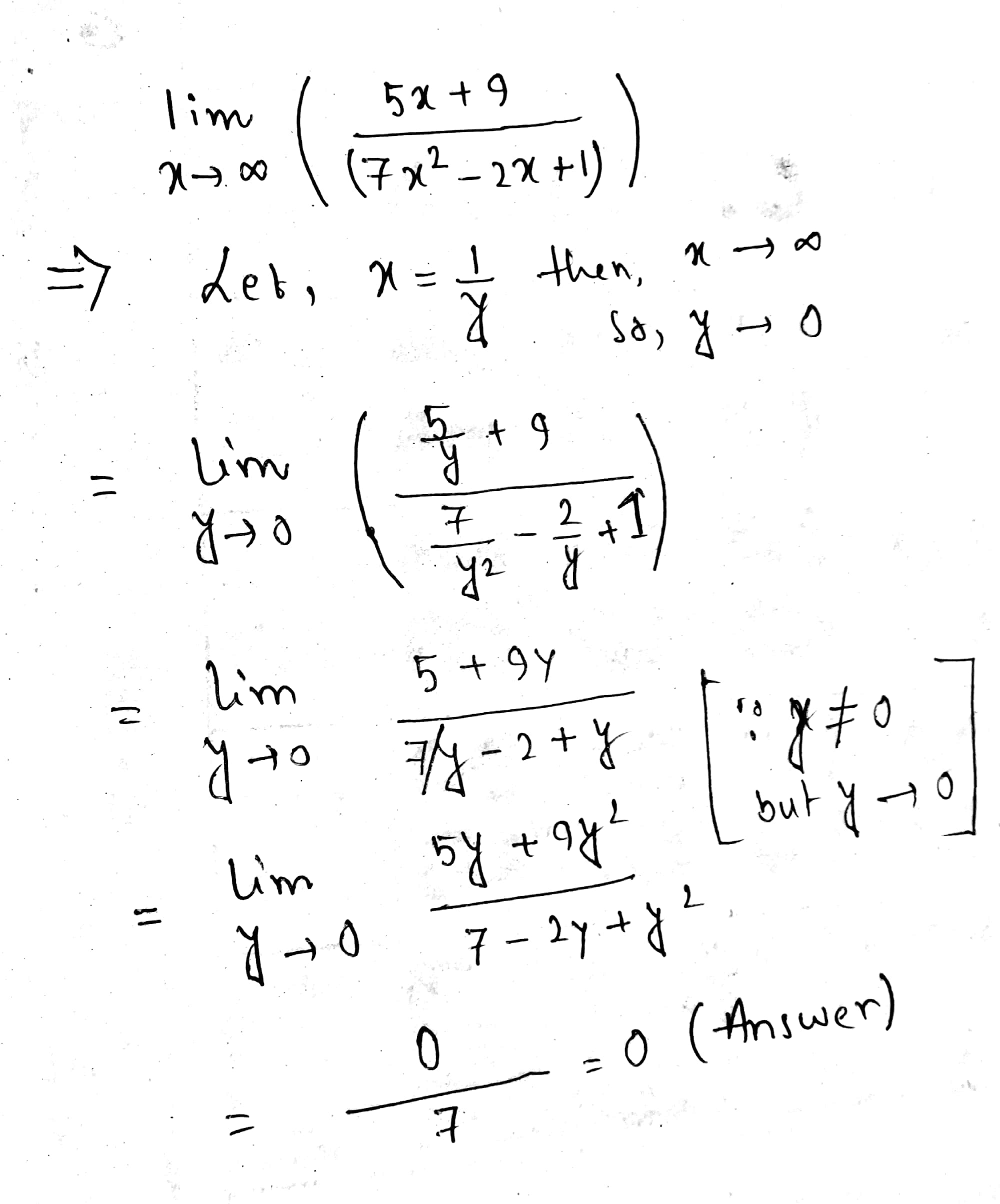
Direct approach... No language. For language , further answer referred.
Hope it helps...
Thank you...



