How do you find points of inflection and determine the intervals of concavity given #y=x^4+x^3-2x^2+1#?
1 Answer
Use the second derivative test.
Explanation:
You can determine the intervals of concavity and inflection points of a function using the second derivative test. The second derivative test tells us whether the slope of the function is increasing or decreasing; when the second derivative is positive, the function is concave up, and, similarly, when the second derivative is negative, the function is concave down.
We'll start by taking the second derivative of the given function, then checking to see at what values of
To find out where
These values are approximately
We will now pick a few "test points" so that we can check to see if the function is increasing or decreasing around these values of
Now, we put these test points into the second derivative of our function and check to see if they yield negative or positive values. If the value is negative, the function is concave down, and if the value is positive, the function is concave up.
I will write
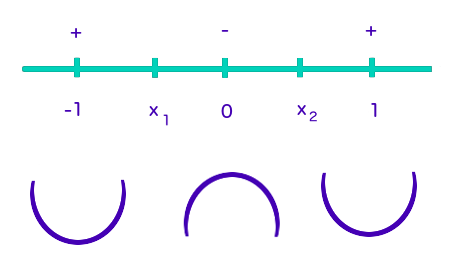
Thus, the function is concave up on the interval
(
And concave down
To find the inflection points, we take the points where the function changes from concave up to concave down and vice versa, and put those
This yields the approximate inflection points (to four decimal places)

