How do you find #sin(pi/12)# and #cos(pi/12)#?
3 Answers
I would use the expansion in series of the two functions, as
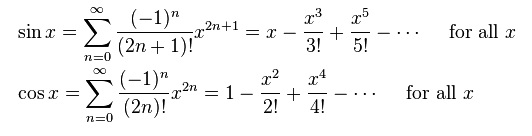
(have a look at the page: http://en.wikipedia.org/wiki/Taylor_series for more info)
Where a function (in a point) is given by an infinite sum of values.
The
We choose few values only, depending upon the accuracy we want (basically, decimal digits you want).
For your case (3 decimals only):
Now you can try to do the same by yourself with
hope it helps
Here is another way to solve this problem.
It's known that
Therefore,
Let's use a formula for a sine of a double angle:
Using this formula,
Substitute for simplicity:
Both are positive (since an angle
Also
We have a system of two equations with two unknowns:
Adding the second equation to the first, we get
Since both
Subtracting the second equation from the first, we get
Since
So, we have a very simple system of two equations with two unknowns:
Adding and subtracting this equations, we find solutions:
Solutions are
Use the cosine and sine half angle formulas:
#sin(theta/2)=+-sqrt((1-cos(theta))/2)# #cos(theta/2)=+-sqrt((1+cos(theta))/2)#
First, let's solve for
#sin((pi/6)/2)=+-sqrt((1-cos(pi/6))/2)#
We will take the positive root since the angle is
#color(blue)(sin(pi/12))=sqrt((1-sqrt3/2)/2)=sqrt((2-sqrt3)/4)color(blue)(=sqrt(2-sqrt3)/2#
The cosine method is almost identical. The positive root will again be taken because cosine is also positive in the first quadrant.
#cos((pi/6)/2)=sqrt((1+cos(pi/6))/2)#
Hence:
#color(red)(cos(pi/12))=sqrt((1+sqrt3/2)/2)=sqrt((2+sqrt3)/4)color(red)(=sqrt(2+sqrt3)/2)#



