How do you find #sinx=1/2#?
3 Answers
Use the trig conversion table and the trig unit circle to solve
Trig table gives
Trig circle gives another arc
Since
They are:
*Diagram not drawn to scale.
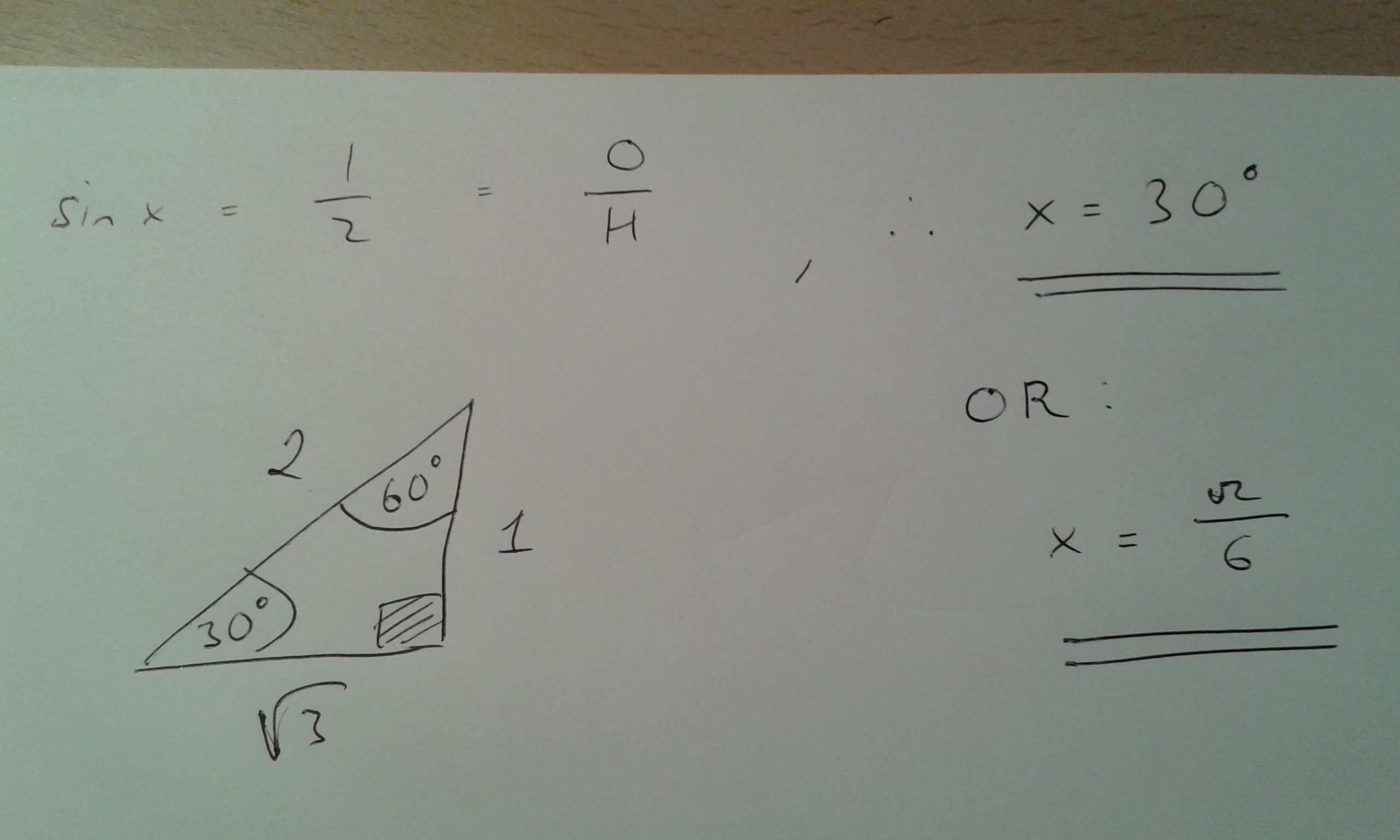
Explanation:
We can find the answer using a triangle or the unit circle
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Using a right triangle
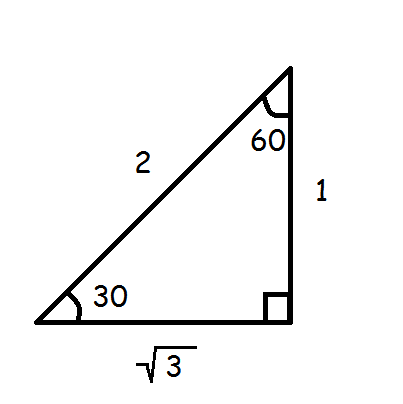
#color(blue)(sin(theta)=1/2#
As we see in the diagram,
So,
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Using unit circle
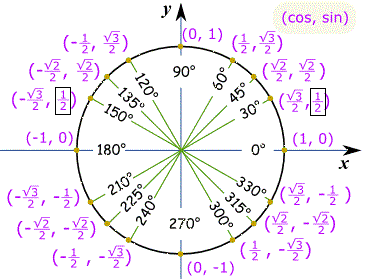
As
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Hope this helps! :)



