How do you find the area of a region using integration?
1 Answer
Let's say we have the following function (
 .
.
Let's say we wanted to know the area from
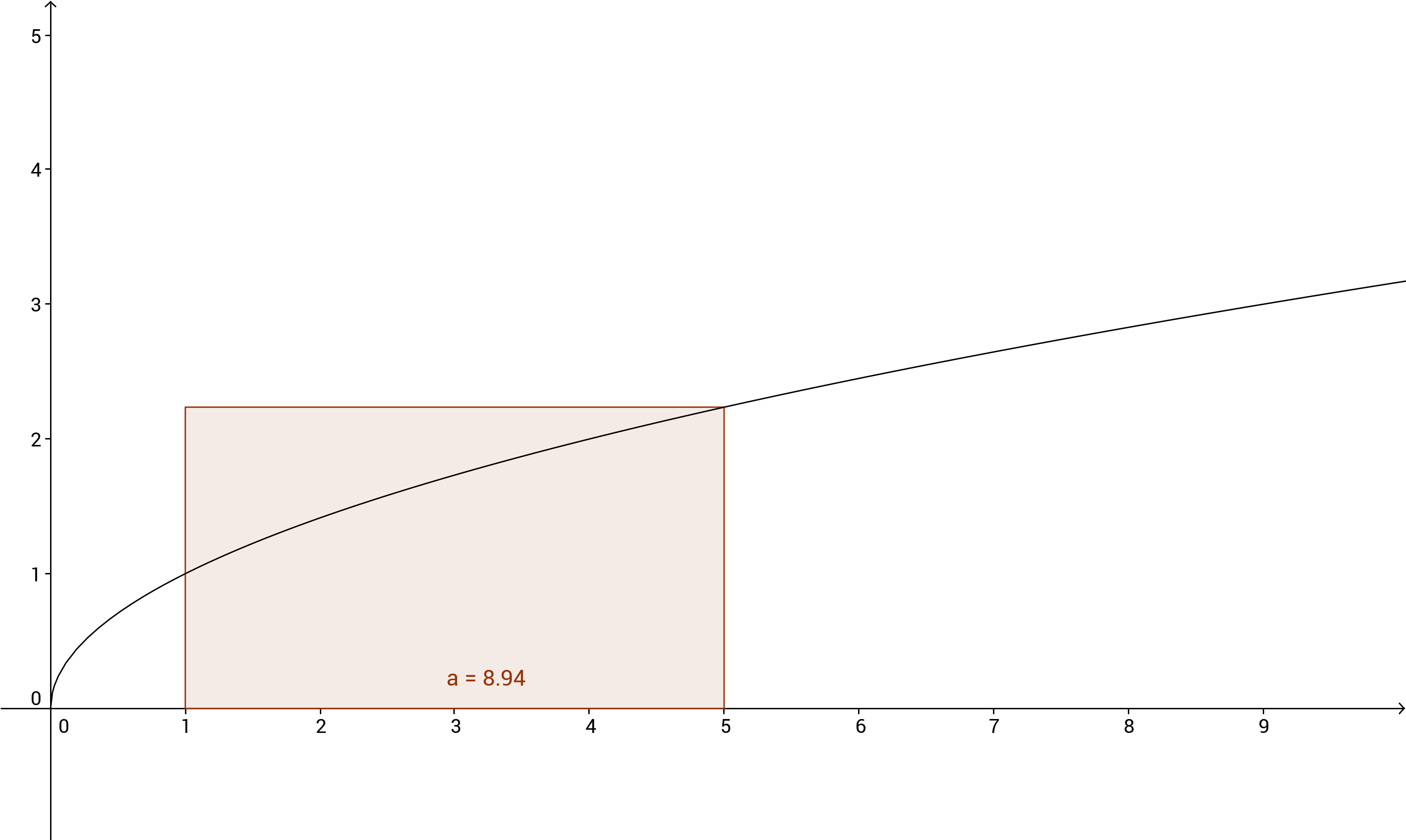
We can calculate the area of this rectangle because we know its width:
This is a bad approximation of the area. There's this excessive part above the function. How could we make this approximation better? We could use another rectangle, like so:
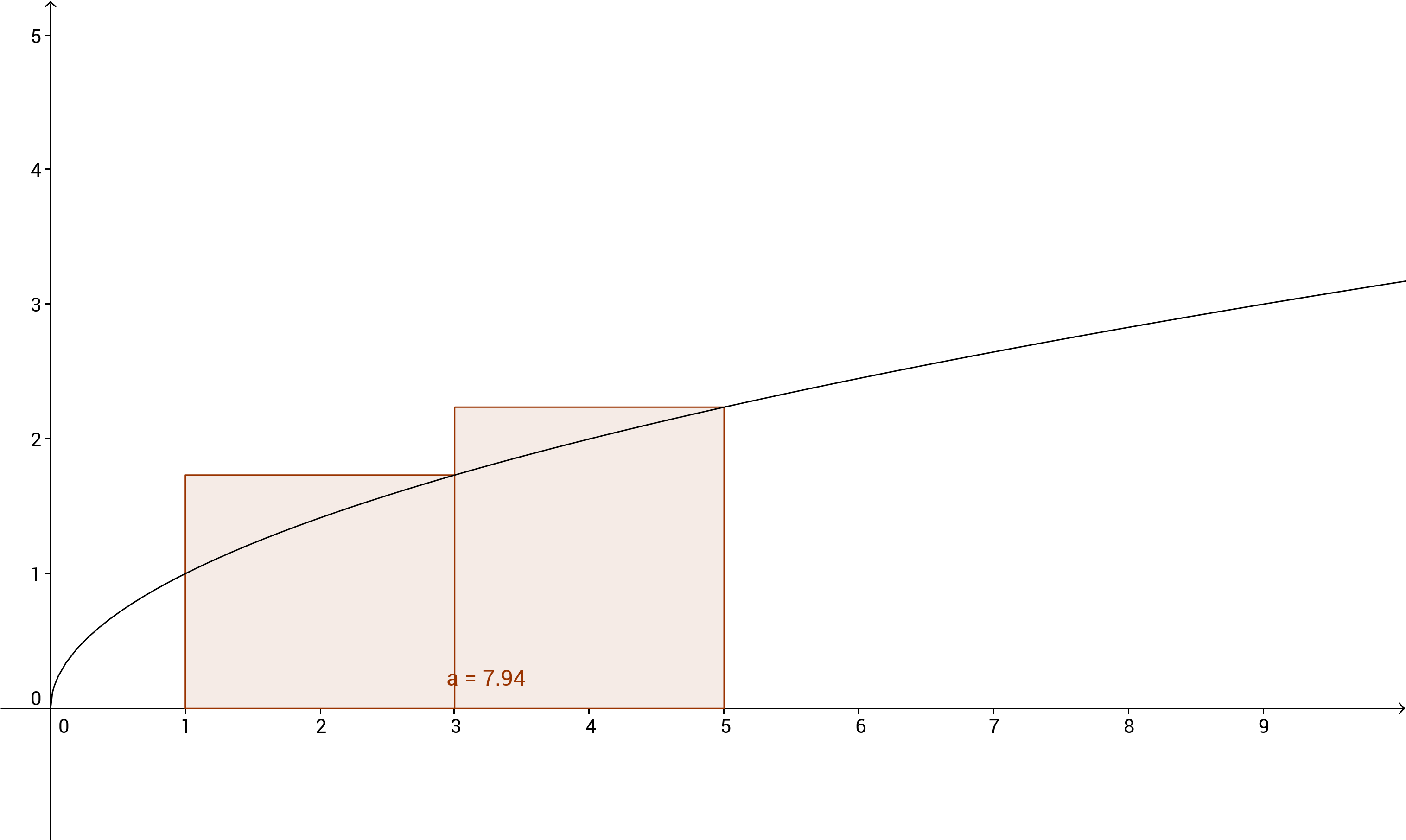
If we add the areas of these two rectangles, we'll get a better approximation, but it will still not even be close to the actual value. We can try using a lot of rectangles, say
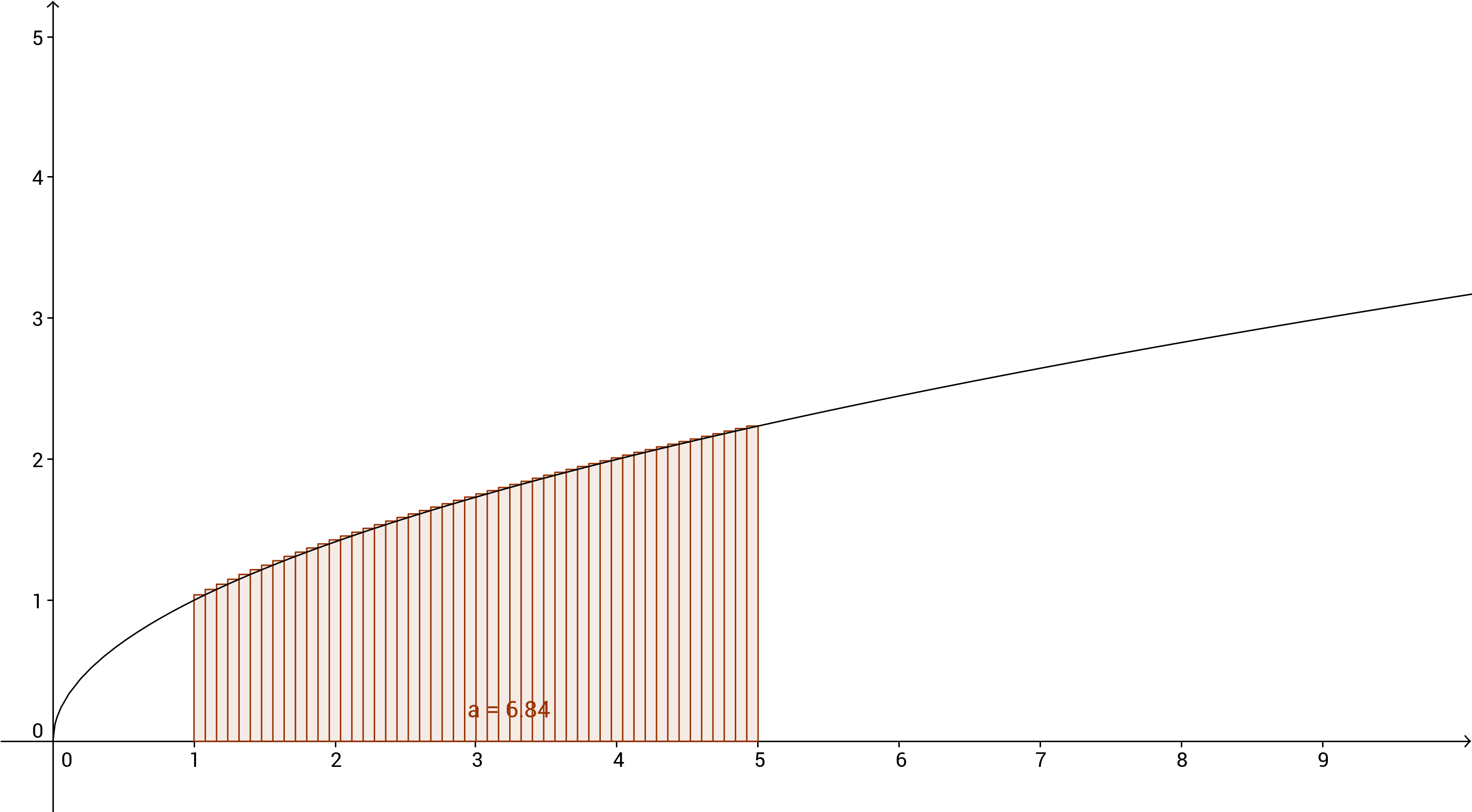
This would take a lot of time to compute, but it would be possible. You'll get a very close approximation to the actual value. What can we do to get the precise area under the function? We can use an infinite amount of rectangles. You can prove (which I am not going to do), that this would give you the area. This infinite summation is called a Riehmann sum.
If you're taking the definite integral of a function, in this case:
So when you're taking the definite integral of a function, you're actually calculating the area under the function.
An indefinite integral is a kind of generalisation of the definite integral. I'll let you first understand definite integrals completely. If you have any questions about indefinite after that, feel free to ask!

