Question

How do you find the area using the trapezoid approximation method, given `1/x^2 dx`, on the interval [1,3] with n=5?

Answer 1

Trapezium rule gives:

`int_1^3 \ 1/x^2 \ dx ~~ 0.69` (2dp)

Explanation:

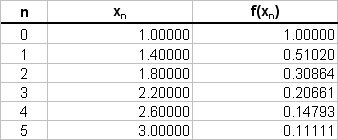
The values of `f(x)=1/x^2-1` are tabulated as follows (using Excel) working to 5dp

Using the trapezoidal rule:

`int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}`

We have:

`int_1^3 \ 1/x^2 \ dx`
`" " ~~ 0.4/2 { 1 + 0.11111 + 2(0.5102 + 0.30864 + 0.20661 + 0.14793) }`

`" " = 0.2 { 1.11111 + 2(1.17339) }`
`" " = 0.2 { 1.11111 + 2.34677 }`
`" " = 0.2 * 3.45788`
`" " = 0.69158`

Let's compare this to the exact value:

`int_1^3 \ 1/x \ dx = [-1/x]_1^3`
`" " = (-1/3) - (-1)`
`" " = 2/3`