How do you find the asymptotes for f(x)= 1/(x^2-2x+1)?
2 Answers
Assymptopes:
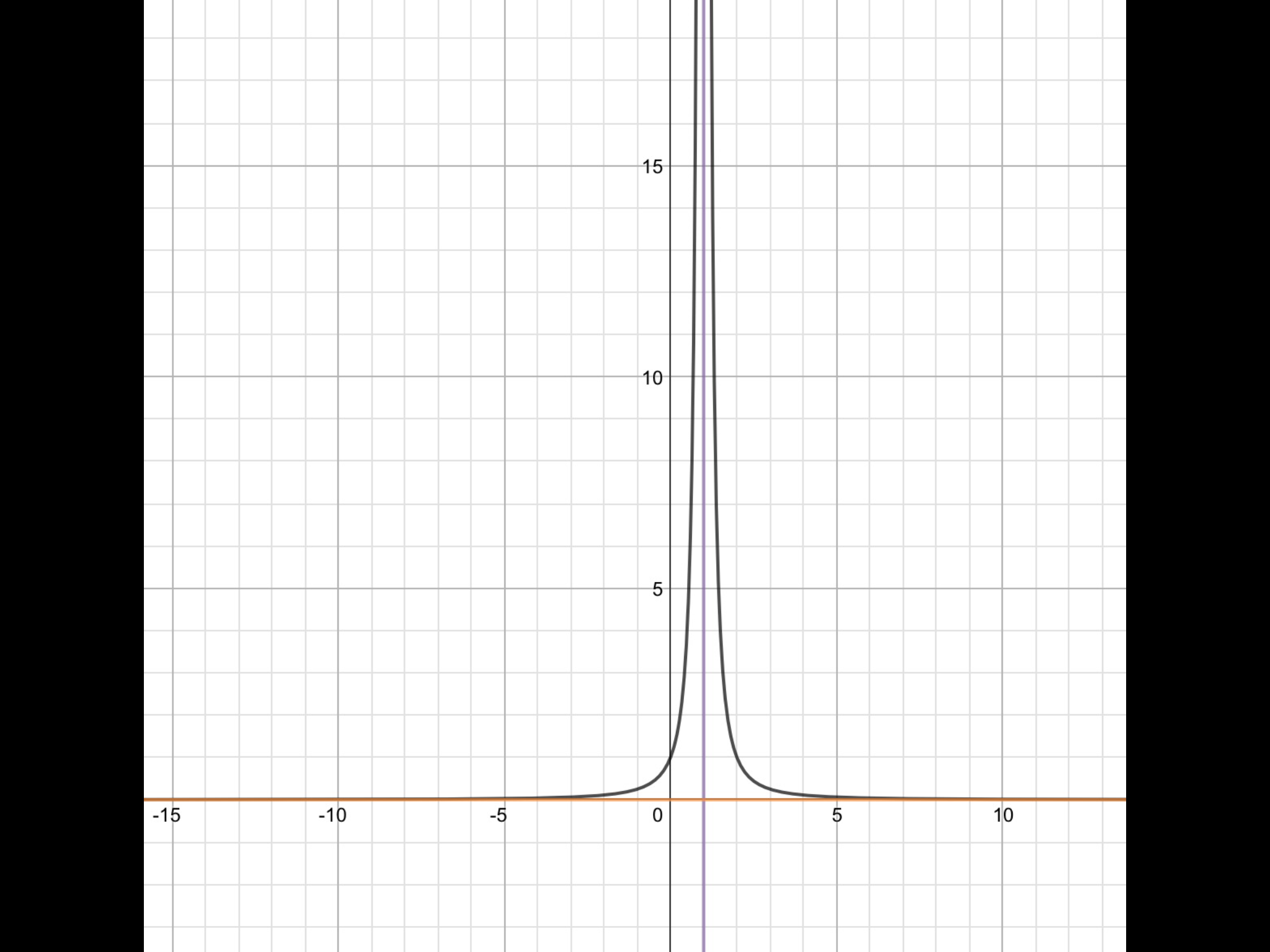
Vertical X=1,
Horizontal Y=0
Explanation:
The Assymptopes of this function is found when the
Denominator expression isn't equal to zero:
Vertical Asymptotes given when denominator isn't equal to zero:
Therefore, Vertical Assymptopes is:
Note finding the, Horizontal Assymptopes requires more logical thinking:
Since when
f(x) > 0 thefore this means that
Horizontal Assymptope: y=0
Explanation:
The denominator of f(x) cannot be zero as this would make f(x) undefined. Equating the denominator to zero and solving gives the value that x cannot be and if the numerator is non-zero for this value then it is a vertical asymptote.
"solve "x^2-2x+1=0rArr(x-1)^2=0
x=1" is the asymptote"
"horizontal asymptotes occur as"
lim_(xto+-oo),f(x)toc" ( a constant)"
"divide all terms on numerator/denominator by the "
"highest power of x that is "x^2
f(x)=(1/x^2)/(x^2/x^2-(2x)/x^2+1/x^2)=(1/x^2)/(1-2/x+1/x^2)
"as "xto+-oo,f(x)to0/(1-0+0)
y=0" is the asymptote"
graph{1/(x^2-2x+1) [-10, 10, -5, 5]}

