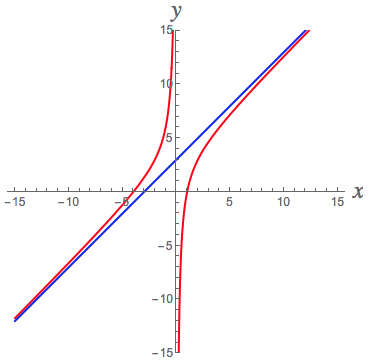
Let #f(x)=(x^2+3x-4)/x=((x+4)(x-1))/x#. Since the #x# in the denominator (bottom) doesn't cancel with any factor in the numerator (top), it follows that #f# has a vertical asymptote at #x=0# (where the denominator is zero).
The function #f(x)=(x^2+3x-4)/x# definitely has a (linear) slant asymptote as #x->\pm \infty# since the degree of the numerator is one more than the degree of the denominator. The linear function representing the slant asymptote can be found as the quotient when doing long division.
If you divide #x# into #x^2+3x-4# using long division, you'll initially get an #x# since #x*x=x^2#. Underneath #x^2+3x-4#, put #x^2=x*x# and subtract to get #3x-4#. Since #3x=3*x#, the next term (on top) in your long division process will be #+3#. Underneath the #3x-4#, put #3x# and subtract to get #-4#. The #-4# is the remainder and the quotient is #x+3#.
In other words:
#f(x)=(x^2+3x-4)/x=x+3+4/x#
Since #4/x->0# as #x->\pm\infty#, it follows that #f(x)\approx x+3# when #x# is large (and the approximation gets better and better...i.e., #f(x)-(x+3)=4/x->0# as #x->\pm\infty#).
Therefore the line #y=x+3# is the slant asymptote.
Here's a picture of this situation: