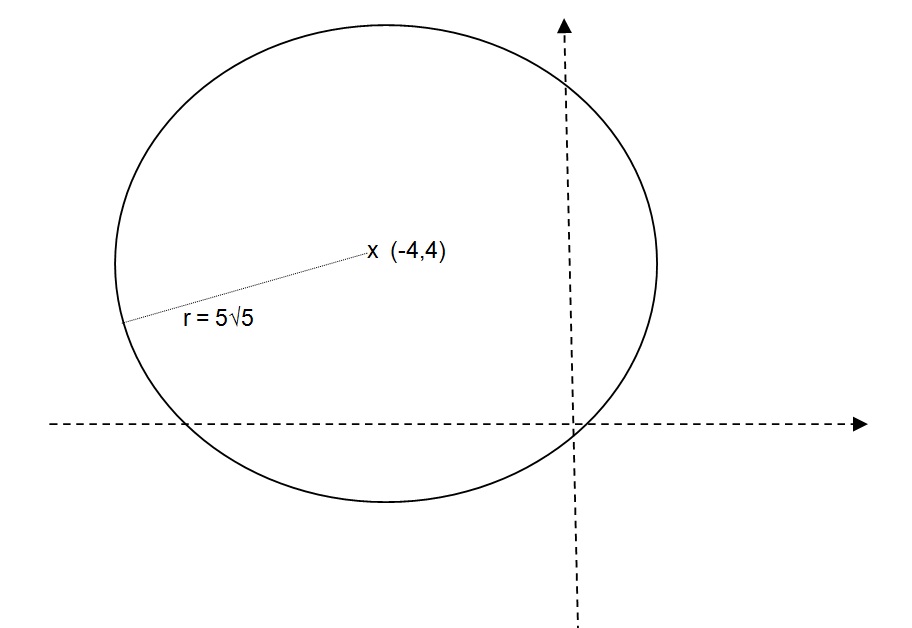
How do you find the center and the radius of the circle; the graph the circle of #x^2+y^2+8x-8y-93=0#?
1 Answer
Jan 20, 2016
The centre is
Explanation:
The standard form of a circle is
To get this equation into the right form, start by grouping like terms.
The centre is