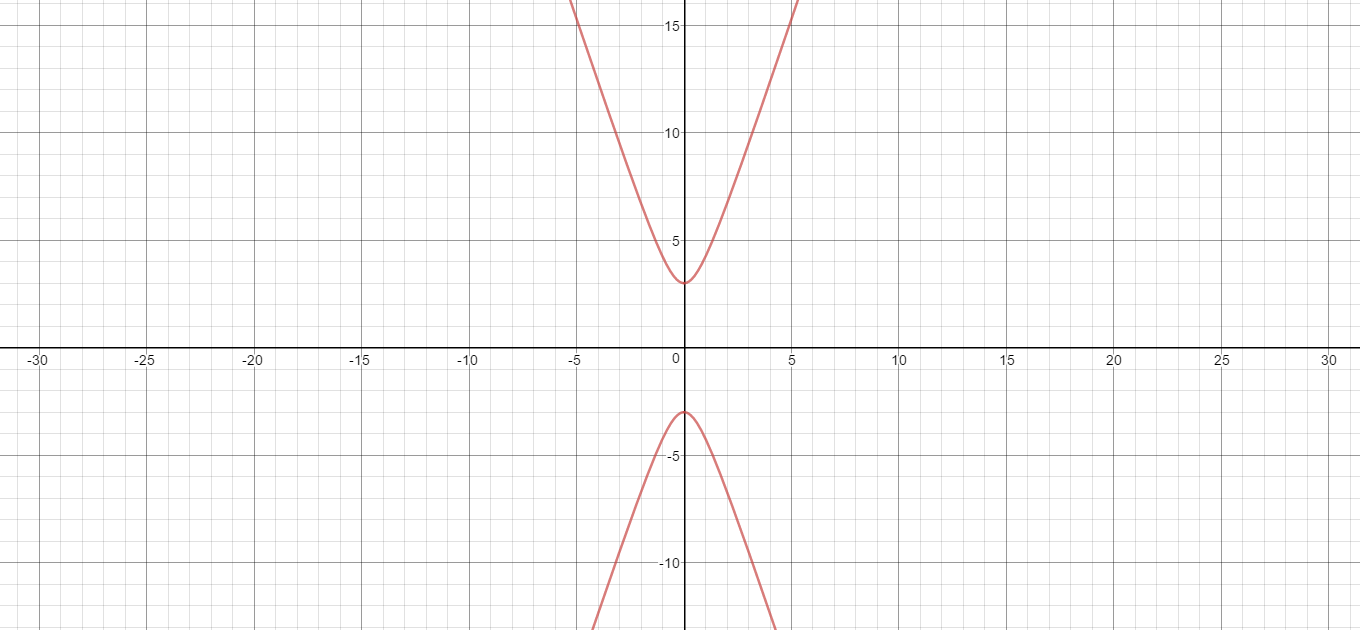
How do you find the center and vertices and sketch the hyperbola #y^2/9-x^2/1=1#?

Question

1790 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-01-06T22:15:42

Please see the explanation.

The center of a hyperbola with an equation of the general form:

#(y - k)^2/a^2 - (x - k)^2/b^2 = 1" [1]"#

is the point #(h, k)#

In the given equation, h and k are obviously 0, therefore, the center is #(0,0)#

Referring, again, to equation [1] the vertices are located at the points:

#(h, k -a) and (h, k + a)#

In the given equation, #a = 3#, therefore, the vertices are located at the points:

#(0, -3) and (0, 3)#

Here is a graph of the hyperbola:

Desmos.com