What do #a# and #b# represent in the equation of a hyperbola?
1 Answer
In the general equation of a hyperbola
Explanation:
For a hyperbola with a horizontal transverse axis,
the general formula is:
For a hyperbola with a vertical transverse axis,
the general formula is:
Note that the
The significance of
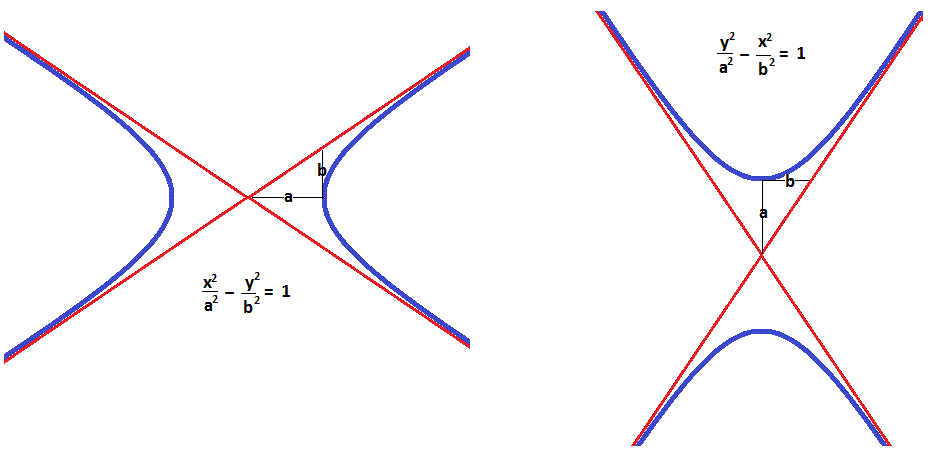
(the
For a hyperbola with a horizontal transverse axis,
the slopes of the two asymptotes are
For a hyperbola with a vertical transverse axis
the slopes of the two asymptotes are
{I hope the reason for this is clear from the above diagrams and the definition of slope.]
