How do you find the center, radius, and equation of a circle with : (1,-2) and (7,6) as the diameter's endpoints?
1 Answer
Jan 26, 2016
Explanation:
The centre of the circle
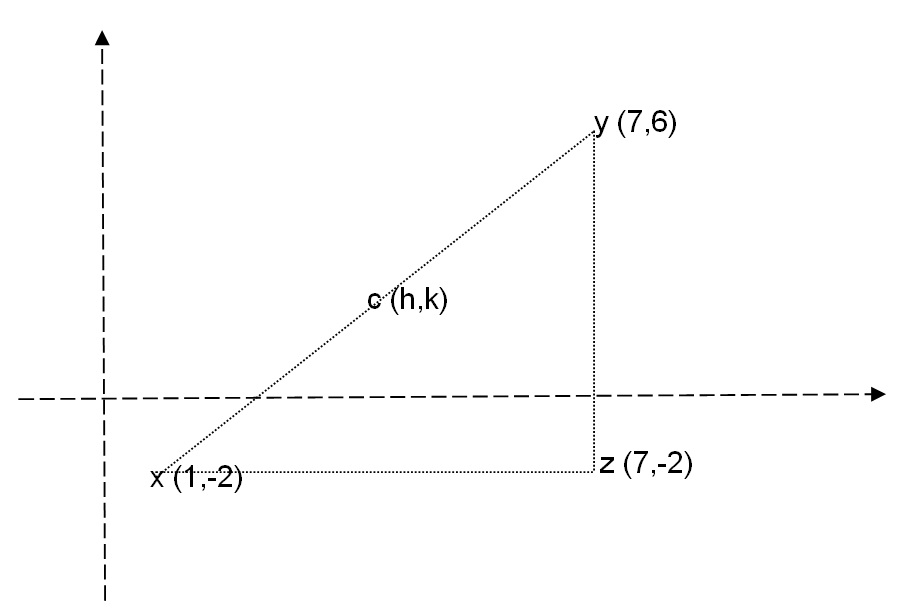
Using Pythagoras to calculate the length of the diameter
The radius is therefore
The equation of the circle is therefore

