How do you find the center, vertices, foci and asymptotes of #4x^2-y^2-24x-4y+28=0#?
1 Answer
Center
Vertex
Foci
Asymptotes
Explanation:
From the given equation
rearrange first so that the variables are together
Perform completing the square
From the form of hyperbola
Center
Vertex
Foci
Asymptotes
and
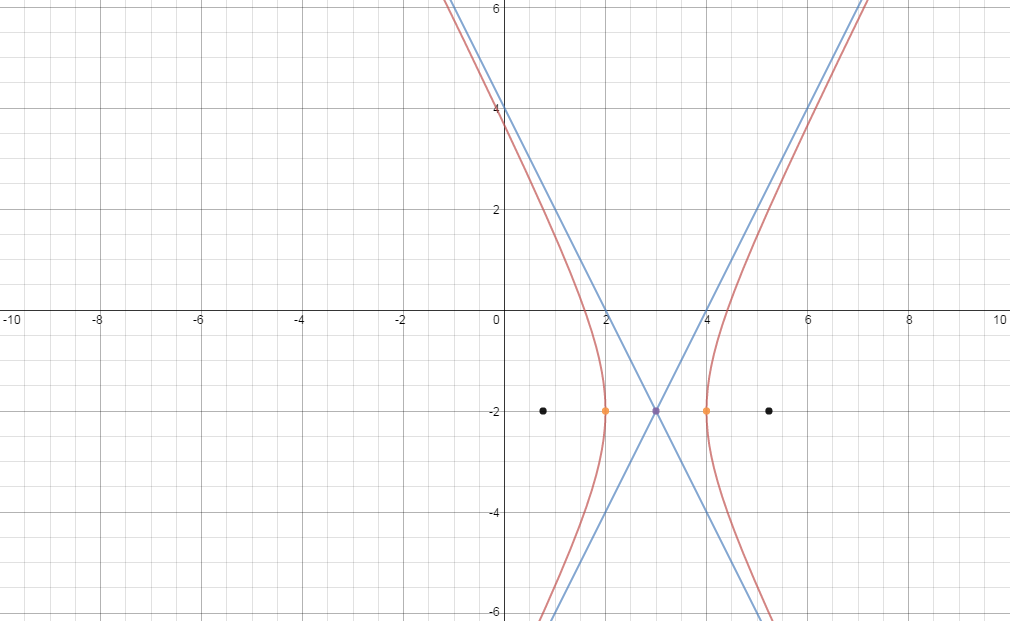
kindly see the graph
hyperbola-colored red
asymptotes-colored blue
center-colored violet
vertices-colored orange
foci-colored black
God bless...I hope the explanation is useful.
