How do you find the centroid of the quarter circle of radius 1 with center at the origin lying in the first quadrant?
1 Answer
Non-Calculus Solution:
Observation 1:
The centroid must lie along the line
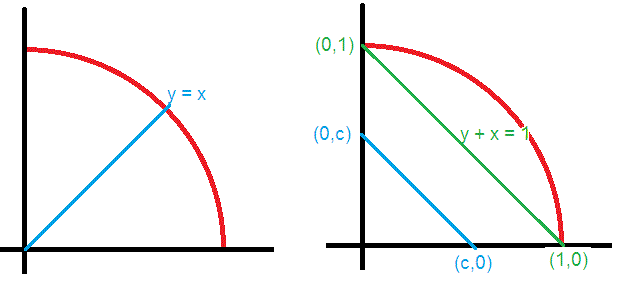
Observation 2:
For some constant,
Observation 3:
Since the area of the quarter circle (with radius =
the line
The area of the triangle formed by the X-axis, the Y-axis, and
is
Therefore
and the centroid is located at the midpoint of the line segment
