Determining the Surface Area of a Solid of Revolution
Key Questions
-
First of all, you are missing a bound. We will assume that the other bound is
#y=0# or the#x# -axis. The answer is#(15pi)/2# .The first step is to determine whether you are rotating along an axis that is parallel to the independent axis or the axis of the parameter (
#x# in this case). And we are not, so this integration should be done with cylindrical shells.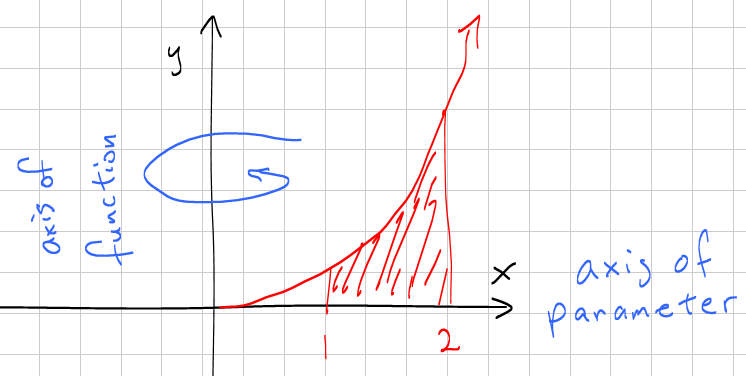
Always draw a diagram to verify what is the parameter and what is the function.You should note that
#y# is not always a parameter of#x# . For instance,#x=y^2# ,#x# is now a parameter of#y# .The formula for cylindrical shells is:
#V=int_a^b2pirhdr#
#h# is represented by#y# , we have#y=x^2# and#y=0#
#r# is represented by#x#
#V=int_1^2 2 pi x (x^2-0) dx# Now that the substitutions are done, we can solve:
#V=2 pi int_1^2x^3dx#
#=2pi (x^4)/4|_1^2#
#=2pi([2^4-1^4])/4#
#=(15pi)/2# -
The answer is
#pi/2[e^2-1]# .Since you are only given a single function and we are rotating about the axis of the parameter, this requires the disk method. The disk method is:
#V=int_a^b Adx#
#=int_a^b pi r^2dx#
#=int_a^b pi [f(x)]^2dx# We have the known values:
#f(x)=e^x#
#a=0#
#b=1# And now we can substitute:
#V=int_0^1 pi (e^x)^2dx#
#=pi int_0^1 e^(2x)dx#
#=pi (e^(2x))/2|_0^1#
#=pi/2[e^2-e^0]#
#=pi/2[e^2-1]# -
If the solid is obtained by rotating the graph of
#y=f(x)# from#x=a# to#x=b# , then the surface area#S# can be found by the integral#S=2pi int_a^b f(x)sqrt{1+[f'(x)]^2}dx#
Questions
Applications of Definite Integrals
-
Solving Separable Differential Equations
-
Slope Fields
-
Exponential Growth and Decay Models
-
Logistic Growth Models
-
Net Change: Motion on a Line
-
Determining the Surface Area of a Solid of Revolution
-
Determining the Length of a Curve
-
Determining the Volume of a Solid of Revolution
-
Determining Work and Fluid Force
-
The Average Value of a Function