How do you find the constant a so that the function is continuous on the entire real line given #f(x)=4, #x <= -1#, ax +b, -1< x <1 and 6, #x>=1#?
1 Answer
We have
Explanation:
We want to find
Strictly speaking we want to find
Just think about what we know so far, and how it would look:
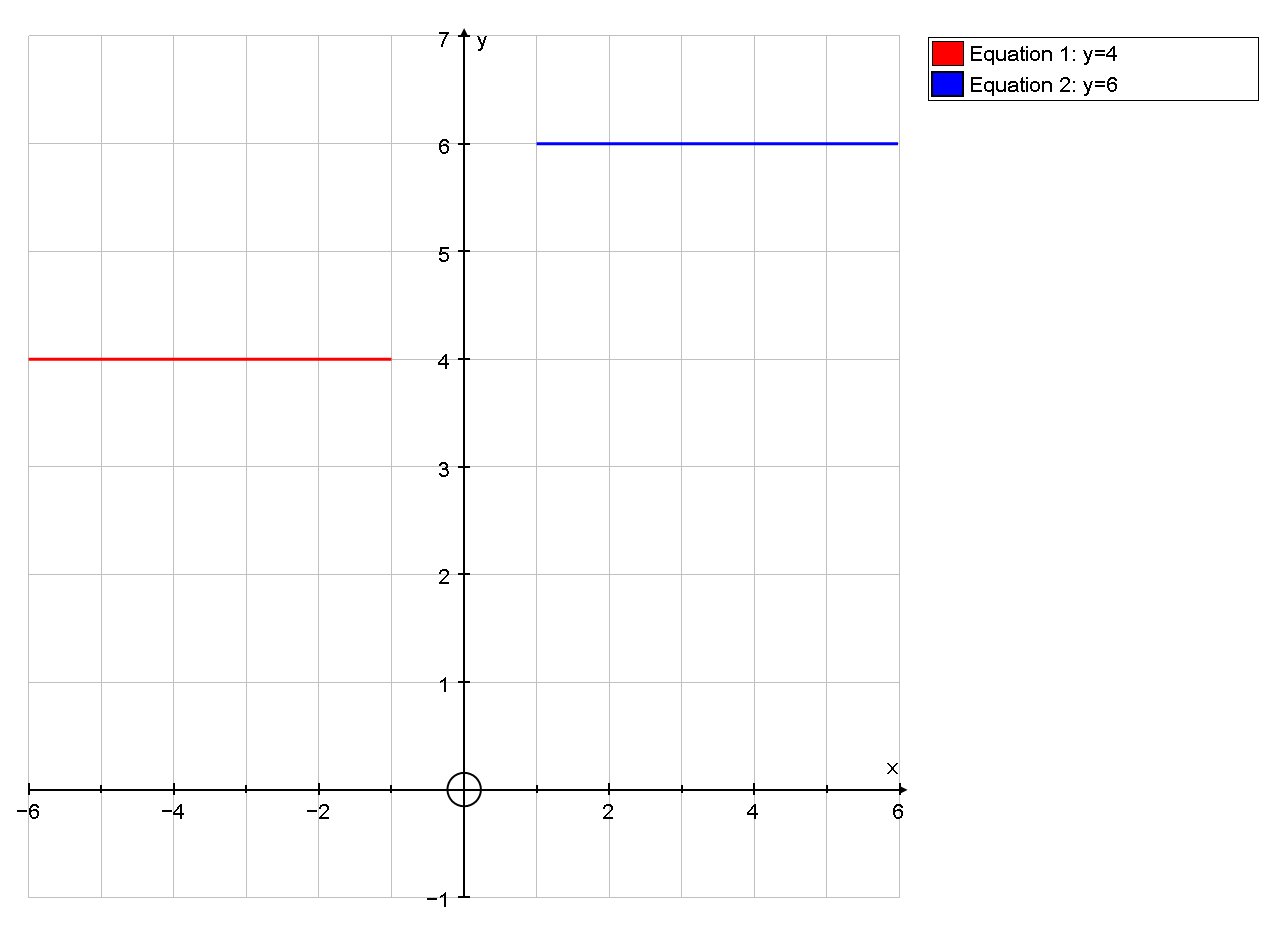
So for the mid interval we need a straight line passing through
This line would have the following gradient:
Hopefully you could also establish that by inspection!
So our required line passes through
Which we can graph to confirm
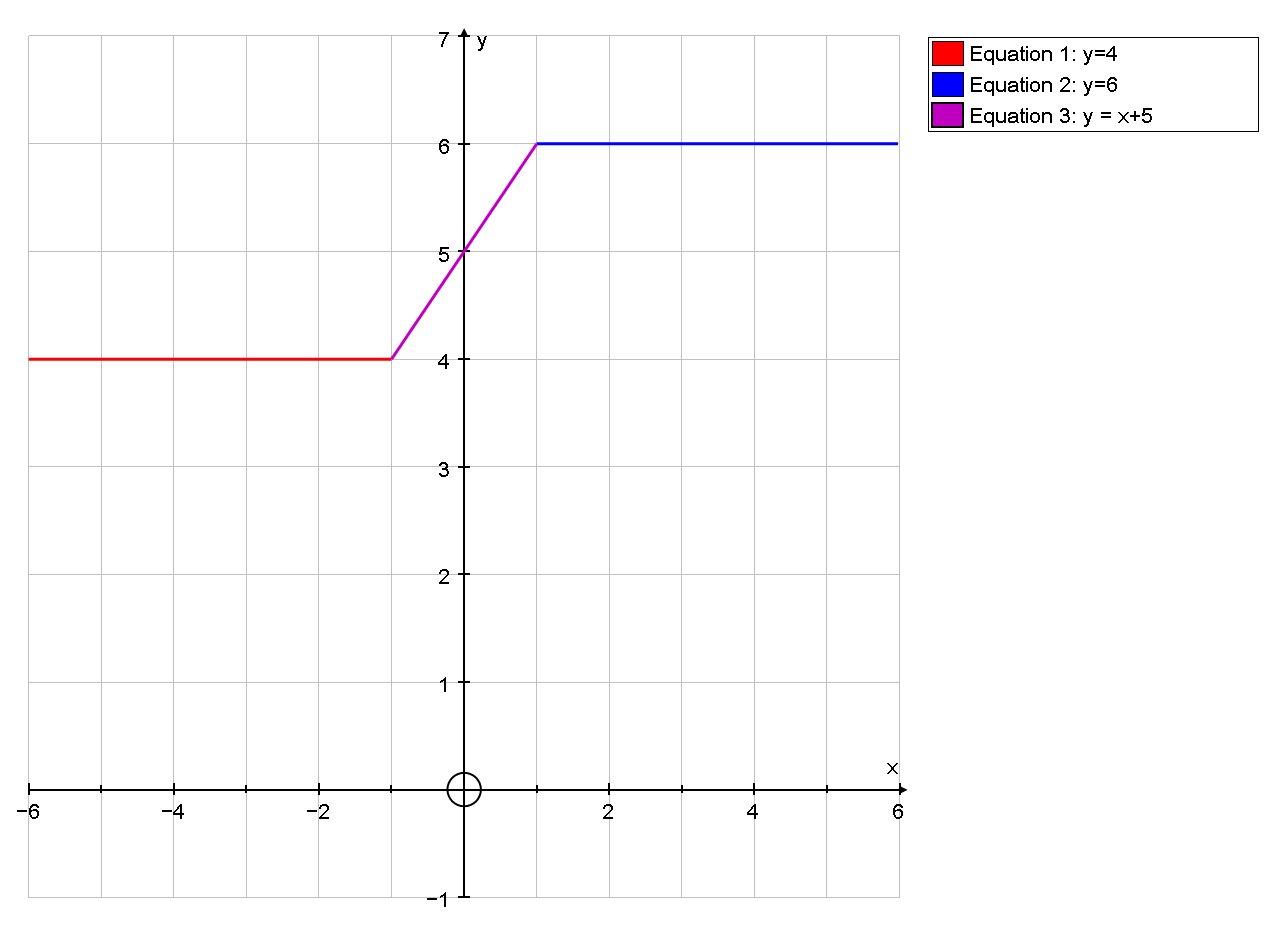
Hence, we have

