Start by factoring out #1/2# in the bracketed part of the equation:
#y=2cos(1/2x+pi/3)-1#
becomes:
#y=2cos(1/2(x+(2pi)/3))-1#
By the five-point method, you need five points to graph the function, #y=2cos(1/2(x+(2pi)/3))-1#. To find the five points, first find the five points for its parent function #y=cosx#. The five main points, #0#, #pi/2#, #pi#, #(2pi)/3#, and #2pi#, including their corresponding y values are listed below.

Now that you have the five points for the parent function, use the mapping rule to apply transformations in order to find the five points for the transformed function, #y=2cos(1/2(x+(2pi)/3))-1#.
Mapping rule: #(color(red)2x-color(blue)((2pi)/3),color(orange)2y-color(green)1)#
#y=2cos(1/2(x+(2pi)/3))-1#
Point #1. ((color(red)2)0-color(blue)((2pi)/3), color(white)(xxx)(color(orange)2)1-color(green)1) rArr color(white)(ixxxxxx)((-2pi)/3,1)#
Point #2. ((color(red)2)pi/2-color(blue)((2pi)/3), color(white)(xx)(color(orange)2)0-color(green)1) rArr color(white)(xxxxxxx)(pi/3,-1)#
Point #3. ((color(red)2)pi-color(blue)((2pi)/3), color(white)(xxx)(color(orange)2)(-1)-color(green)1) rArr color(white)(xxx)((4pi)/3,-3)#
Point #4. ((color(red)2)(3pi)/2-color(blue)((2pi)/3), color(white)(ix)(color(orange)2)0-color(green)1) rArr color(white)(xxxxxxx)((7pi)/3,-1)#
Point #5. ((color(red)2)2pi-color(blue)((2pi)/3), color(white)(xx)(color(orange)2)1-color(green)1) rArr color(white)(xxxxxxx)((10pi)/3,1)#
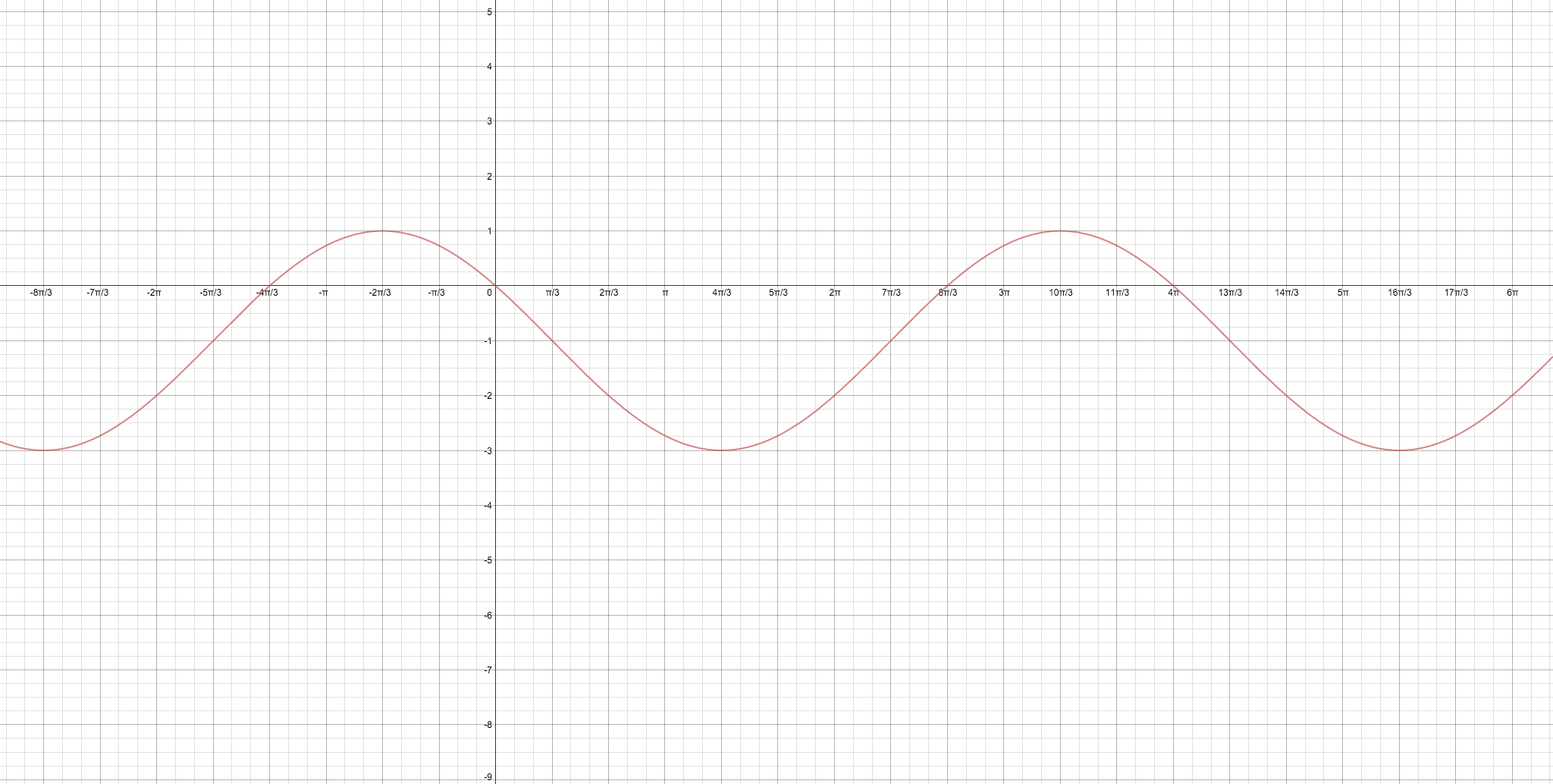
Zoom in to check the five main points shown on the graph.



