How do you find the definite integral of #int (x^2-2)/(x+1)# from #[0,2]#?

Question

23365 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-01-07T22:17:16

#-ln3#

Start by dividing the numerator by the denominator using long or synthetic division.

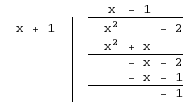
enter image source here

Thus:

#int_0^2(x^2 - 2)/(x + 1)dx = int_0^2 x - 1 + -1/(x + 1)dx#

We can integrate using the rules #int(1/x)dx= ln|x| + C# and #int(x^n)dx = x^(n +1)/(n + 1) + C#.

#= [1/2x^2 - x - ln|x + 1|]_0^2#

Evaluate using #int_a^b F(x) = f(b) - f(a)#, where #f'(x) = F(x)#.

#=1/2(2)^2 - 2 - ln|3| - (1/2(0)^2 - 0 - ln|0 + 1|)#

#=1/2(4) - 2 - ln|3| - 0#

#= -ln3#

In celebration of this being the 2000th answer I ever wrote for socratic, I've included a whole bunch of practice exercises for your improvement

Practice exercises

a) #int_1^4 (x^3 + 7x + 14)/(x + 2)dx#

b) #int_7^15 (2x^4 - 18x^3 + 2x^2 - 5x + 1)/(2x + 1)#

c) #int_3^6 (5x^5 + 2x^2 - 8)/(2(x + 4))#

Bonus
Hint: Use substitution
b) #int_e^(e + 3) (e^(2x) - e^x)/sqrt(e^x) dx#

Hopefully this helps!

Answers to practice exercises:
#1. 33#
#2. 2920#
#3. 2102#
bonus: #3474#