Question

How do you find the derivative of `y = tanx + cotx`?

Answer 1

`f'(x)=sec^2(x)-csc^2(x)`

Explanation:

Treat the tanx separately and the cotx separately. Don't forget the derivatives for trig functions:

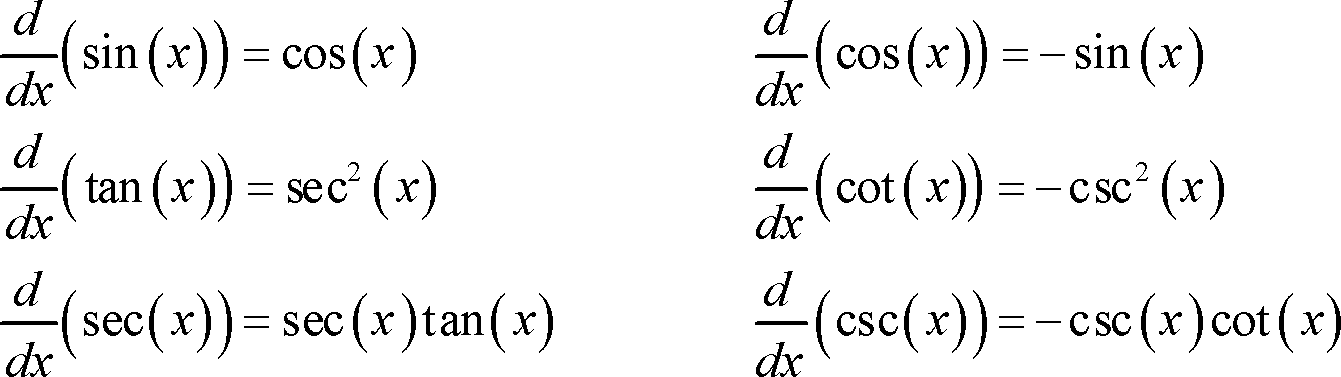
Derivative of `tanx` is `sec^2x`. Derivative of `cotx` is `-csc^2x`. Since they are adding together, we can treat them it as `tan'x` and `cot'(x)`:

`f'(x)=sec^2(x)-csc^2(x)`

Answer 2

`y' = -cos2xsec^2xcsc^2x`

Explanation:

A bit of a different approach...

Rewrite in terms of sine and cosine.

`y = sinx/cosx + cosx/sinx`

`y = (sin^2x + cos^2x)/(sinxcosx)`

`y = 1/(sinxcosx)`

`y = (sinxcosx)^-1`

Now use the chain rule to differentiate. Let `y = u^-1` and `u = sinxcosx`. The function `u` can be differentiated using the product rule to `(du)/dx = cosx(cosx) + sinx(-sinx) = cos^2x - sin^2x = cos2x`. By the power rule, `dy/(du) = -1/u^2`.

`y' = dy/(du) * (du)/dx`

`y' = cos2x * -1/u^2`

`y' = -cos(2x)/(sinxcosx)^2`

`y' = -cos2xsec^2xcsc^2x`

Hopefully this helps!