How do you find the determinant of #|(4,6,7),(3,-2,-4), (1,1,1)|#?

Question

2139 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-08-03T23:48:54

The Rule of Sarrus! -> #det(A) = 1#

Order three determinants follow The Rule of Sarrus . Consider a matrix

#A = |(a_1,a_2,a_3),(a_4,a_5,a_6), (a_7,a_8,a_9)|#

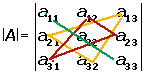
The Rule of Sarrus says:

#det(A) = |A| = a_1 a_5 a_9 + a_2 a_6 a_7 + a_3 a_4 a_8 - a_3 a_5 a_7 - a_6 a_8 a_1 - a_9 a_4 a_2#

These pictures may help in understanding what this rule does:

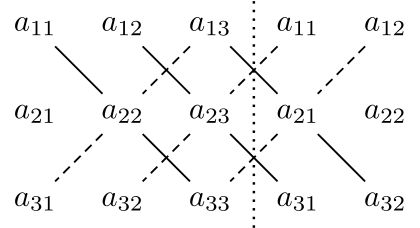
enter image source here

Positive sign:
enter image source here

Negative sign:
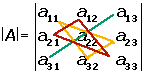
enter image source here

In your case:

#|A| = -8 - 24 + 21 + 14 + 16 - 18 = 1#