The answer is: #r=4/3sqrt2#, #h=8/3#
We can imagine a vertical section of the figure, that would appear:
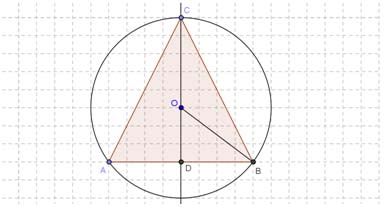
Let #r# be the radius of the cone, #R# be the radius of the sphere and #h# be the height of the cone.
Let's put #DhatOB=x# with limitations #0<=x<=pi#.
In the right-angled triangle #DOB#:
#r=DB=Rsinx#, #OD=Rcosx#, than
#h=CD=OC+OD=R+Rcosx=R(1+cosx)#.
So the volume of the cone is:
#V=1/3pir^2hrArrV=1/3pi(Rsinx)^2*R(1+cosx)rArr#
#V=1/3piR^3sin^2x(1+cosx)#
#V'=1/3piR^3*[2sinx*cosx*(1+cosx)+sin^2x(-sinx)]=#
#=1/3piR^3sinx[2cosx(1+cosx)-sin^2x]=#
#=1/3piR^3sinx(2cosx+2cos^2x-sin^2x)=#
#=1/3piR^3sinx(2cosx+2cos^2x-1+cos^2x)=#
#=1/3piR^3sinx(3cos^2x+2cosx-1)#
Now let's find the signum of the derivative, since #sinx>=0# for every #x# in the limitations, than:
#V'>=0rArr3cos^2x+2cosx-1>=0rArr#
#Delta/4=(b/2)^2-ac=1+3=4#
#cosx=((-b/2)+-sqrt(Delta/4))/a=(-1+-2)/3#,
So:
#cosx<=-1vvcosx>=1/3#
The first one has only the solution:
#x=pi#,
the second:
#-arccos(1/3)<=x<=arccos(1/3)#, but for the limitations:
#0<=x<=arccos(1/3)#.
The function growths from zero to #arccos(1/3)#, than it decreases.
So #x=arccos(1/3)# is the maximum requested.
Let's find now #r# and #h#:
#r=Rsinx=Rsqrt(1-cos^2x)=2sqrt(1-(1/3)^2)=2sqrt(1-1/9)=#
#=2sqrt((9-1)/9)=2sqrt(8/9)=2*2sqrt2/3=4/3sqrt2#
#h=R(1+cosx)=2(1+1/3)=2((3+1)/3)=8/3#.


