Question

How do you find the domain and range and determine whether the relation is a function given :`x=2y^2-3`?

Answer 1

See below.

Explanation:

For y as a function of x.

`x = 2y^2 -3`

Rearrange;

Add 3 to both sides:

`2y^2 = x + 3`

Divide by 2:

`y^2 = 1/2x + 3/2 => y^2 = (x + 3)/2`

Taking roots of both sides:

`y = sqrt((x + 3)/2)`

For positive root:

For the domain we must make sure the numerator is `>= 0`, since we are only interested in real numbers.

The numerator is `>=0` for `x >= -3`

So the domain is `{ x in RR | x >= -3 }`

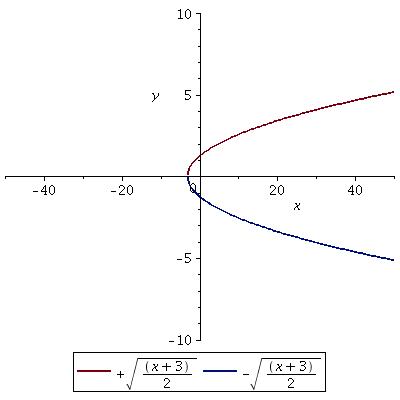
The range for the positive root is:

As
`x -> +oo`
`y -> +oo`

So the range is:

`{y in RR | y >= 0 }`

For negative root the domain is the same for real numbers. The range is in the reverse direction:

`{ y in RR | y <= 0 }`

The determination of a function.

For positive root only a function is defined.
For negative root only a function is defined.

For `+-sqrt((3 + x )/2 )`

This is not a function. A function is only defined if an element in a domain is mapped onto one and one only element in a range. In the case of both roots this would map one element in the domain to two elements in the range. This is sometimes called a one to many relationship.

See graph: