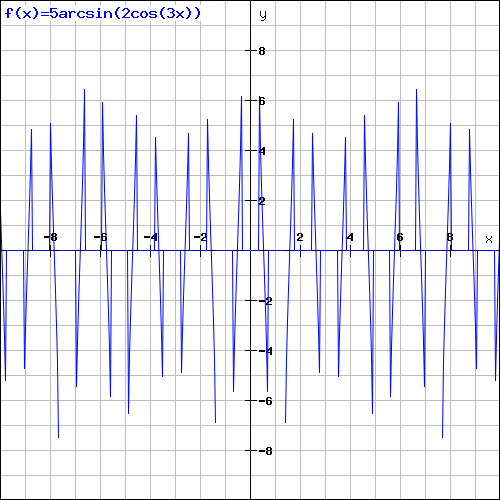
#arcsin(x):[-1,1]->[-pi/2,pi/2]#
So the argument of the function must be between 1 and -1.
#-1<=2cos(3x)<=1#
So we have to solve the system:
#{(2cos(3x)>=-1),(2cos(3x)<=1):}#
#{(cos(3x)>=-1/2),(cos(3x)<=1/2):}#
#pi/3+2kpi<=3x<=2/3pi+2kpi vv 4/3pi+2kpi<=3x<=5/3pi+2kpi#
So, isolating x, the domain would be:
#pi/9+2/3kpi<=x<=2/9pi+2/3kpi vv 4/9pi+2/3kpi<=x<=5/9pi+2/3kpi#.
Considering that #2cos(3x)# in the domain would vary in #[-1,1]#, the range of #arcsin(x)# willl vary in #[-pi/2,pi/2]#. But the function has a cohefficient "5" that extends the amplitude of our function to #-5/2pi,5/2pi#.
This strange function would be something like this: