How do you find the domain and range of #1/sqrt(8-t)#?
1 Answer
Dec 1, 2017
Domain: All
Range: All
Explanation:
The domain is simply the values
For the above function, dividing by
We can express that in interval notation as
As for the range, we can plot the graph and find it from that.
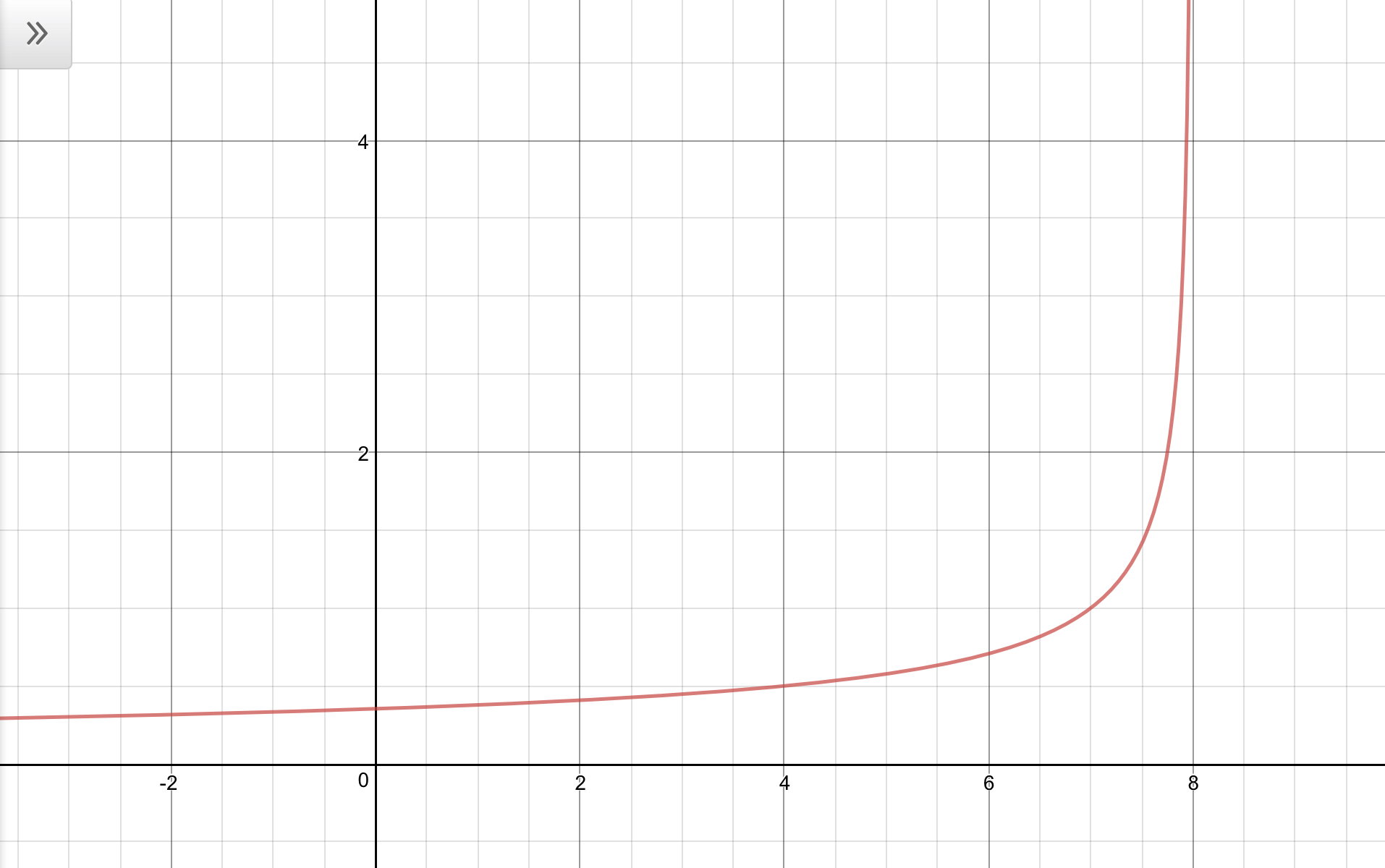
We can see the graph starts just above
So we can express the range as

