How do you find the end behavior of a quadratic function?
1 Answer
Quadratic functions have graphs called parabolas. 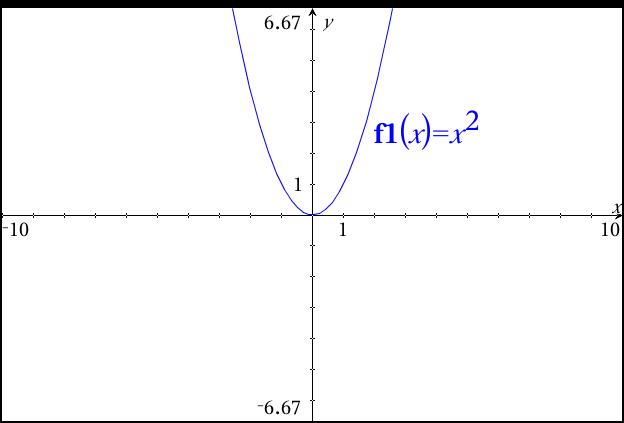
The first graph of y =
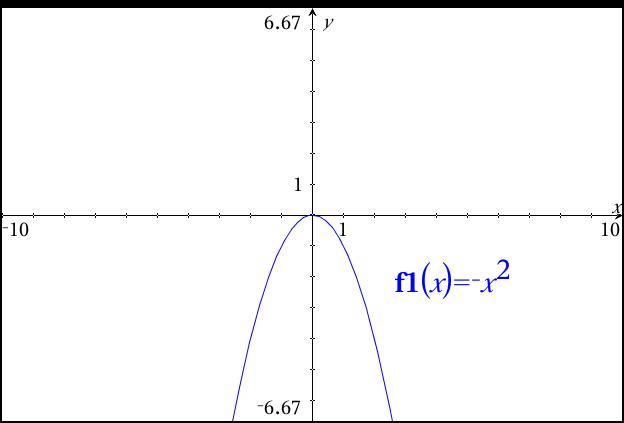
Compare this behavior to that of the second graph, f(x) =
Both ends of this function point downward to negative infinity. The lead coefficient is negative this time.
Now, whenever you see a quadratic function with lead coefficient positive, you can predict its end behavior as both ends up. You can write: as
as
Last example:
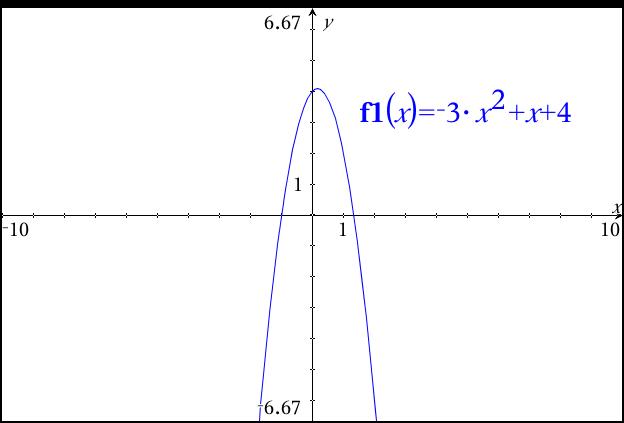
Its end behavior:
as
(right end down, left end down)

