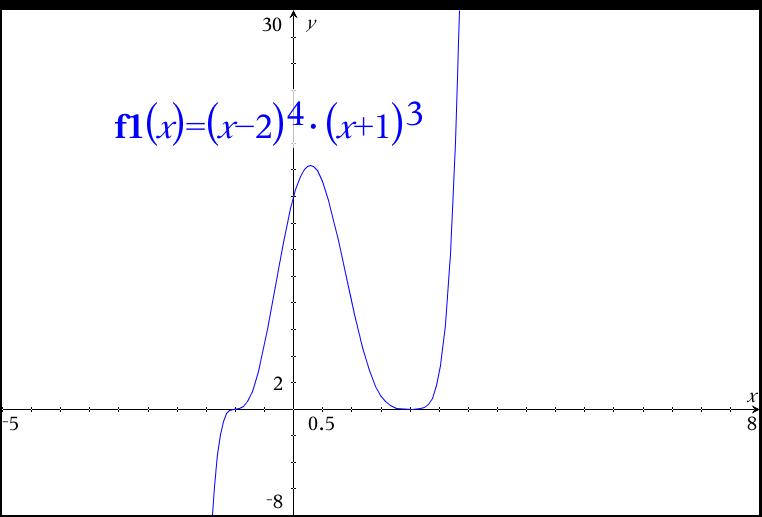
What is the end behavior of #f(x) = (x - 2)^4(x + 1)^3#?
1 Answer
For any polynomial function that is factored, use the Zero Product Property to solve for the zeros (x-intercepts) of the graph. For this function, x = 2 or -1.
For factors that appear an even number of times like
For factors that appear an odd number of times, the function will run right through the x-axis at that point. For this function, x = -1.
If you multiply the factors out, your term of highest degree will be
Here is the graph: