The circle equation is
#c(x,y) = (x-x_0)^2+(y-y_0)^2-r^2 = 0#
and the parabola
#p(x,y) = y^2-4x=0#
At tangency point both curves have the same declivity or the same orientation in their normal vectors. Let #p_t = {x_t,y_t} = {1,2}# their tangency point. At this point
#grad c(x_t,y_t) + lambda grad p(x_t,y_t) = vec 0#
where
#grad c(x_t,y_t)={2(x_t-x_0),2(y_t-y_0)}# and
#grad p(x_t,y_t) = {-4,2y_t}#
and also
#c(x_t,y_t) = (x_t-x_0)^2+(y_t-y_0)^2-r^2 = 0#
Solving
#{
(2(x_t-x_0) =-4 lambda),
(2(y_t-x_0)=2 lambda y_t),
( (x_t-x_0)^2+(y_t-y_0)^2-r^2 = 0)
:}#
for #x_0,y_0,lambda# we obtain
#(
(x_0 = 1 - 2 sqrt[2], y_0 = 2 (1 + sqrt[2]), lambda = sqrt[2]),
(x_0 = 1 + 2 sqrt[2], y_0 = 2 (1 - sqrt[2]), lambda = -sqrt[2]))
#
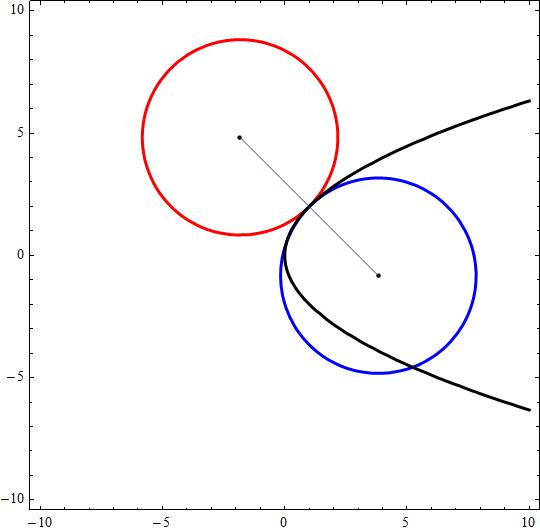
Attached a figure showing the two solutions.